Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 230
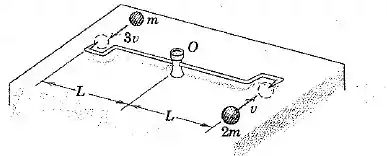
As pequenas esferas, que possuem as massas e velocidades iniciais indicadas na figura, atingem e tornam-se presas às extremidades pontudas da haste, que é livremente articulada em e está inicialmente em repouso. Determine a velocidade angular do conjunto após o impacto. Despreze a massa da haste.
Passo 1
Bom galera, nesse exercício queremos encontrar a velocidade angular do conjunto após o impacto. Sabemos que como a quantidade de movimento angular se conserva, podemos escrever
Passo 2
Por definição, temos que . Dessa forma, substituindo na equação, temos
Passo 3
Agora, para encontrar a velocidade angular do conjunto basta isolar , ficando com
Resposta
Exercícios de Livros Relacionados
Em um dado instante, a partícula de massa m tem a posição e a velocidade mostradas na figura, e sofre a ação da força F . Determine sua quantidade de movimento angular em torno do ponto O e a taxa de
O conjunto parte do repouso e atinge uma velocidade angular de 150r p m sob a ação de uma força T de 20N aplicada à corda por t segundos. Determine t . Despreze o atrito e todas as massas exceto a das
A esfera de 3k g se desloca no plano x - y e tem a velocidade indicada em um determinado instante. Determine sua ( a ) quantidade de movimento linear, ( b ) quantidade de movimento angular em torno do
A única força atuando sobre um satélite da Terra que se desloca fora da atmosfera terrestre é a atração gravitacional radial. O momento desta força é nulo em torno do centro da Terra tomado como um po
A esfera de 6k g e o bloco de 4k g (mostrado em corte) estão presos ao braço de massa desprezível que gira no plano vertical em torno de um eixo horizontal em O . O tampão de 2k g é liberado a partir