Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 236
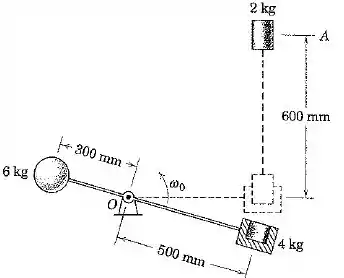
A esfera de e o bloco de (mostrado em corte) estão presos ao braço de massa desprezível que gira no plano vertical em torno de um eixo horizontal em . O tampão de é liberado a partir do repouso em e cai dentro do recesso no bloco quando o braço atinge a posição horizontal. Um instante antes da união, o braço tem uma velocidade angular . Determine a velocidade angular do braço imediatamente após o tampão ter se prendido no bloco.
Passo 1
Bom galera, nesse exercício queremos encontrar a velocidade angular do braço. Sabemos que
Como a quantidade de movimento angular se conserva, temos que
Passo 2
Podemos então escrever
Por definição, temos que
Passo 3
Substituindo na equação a relação para os valores iniciais e finais, temos
Isolando , ficamos com
Resposta
Exercícios de Livros Relacionados
Uma centrífuga é constituída por quatro recipientes cilíndricos, cada um com massa m , a uma distância radial r a partir do eixo de rotação. Determine o tempo t necessário para levar a centrífuga a um
As três pequenas esferas estão soldadas à estrutura leve rígida que está girando em um plano horizontal em torno de um eixo vertical através de O com uma velocidade angular θ ˙ = 20r a d / s . Se um t
Duas esferas de aço, cada uma com massa m , estão soldadas a uma haste leve de comprimento L e massa desprezível e estão inicialmente em repouso sobre uma superfície horizontal lisa. Uma força horizon
O carrinho de massa 2 m é livre para se mover ao longo dos trilhos horizontais e transporta as duas esferas, cada uma com massa m , montadas sobre as hastes de comprimento l e massa desprezível. O eix
Os carros de um passeio de montanha-russa possuem uma velocidade de 30k m / h quando passam pelo topo do trilho circular. Despreze qualquer atrito e calcule suas velocidades v quando atingem a posição