Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 233
O conjunto parte do repouso e atinge uma velocidade angular de sob a ação de uma força de aplicada à corda por segundos. Determine . Despreze o atrito e todas as massas exceto a das quatro esferas de , que podem ser tratadas como partículas.
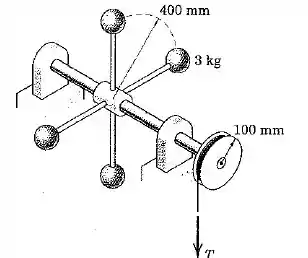
Passo 1
Bom galera, nesse exercício queremos encontrar o tempo especificado. Para isso, utilizaremos a quantidade de movimento angular. Sabemos que a quantidade de movimento angular se conserva, dessa forma, podemos escrever
Passo 2
Substituindo com base nas informações fornecidas, temos que
Passo 3
Ao solucionar a integral e substituir os valores de e , chegamos em
Isolando , temos
Resposta
Exercícios de Livros Relacionados
Determine o módulo H O da quantidade de movimento angular em torno do ponto de lançamento O do projétil de massa m , que é lançado com velocidade v 0 no ângulo θ conforme indicado ( a ) no instante do
A esfera de 0,2k g e seu cordão de sustentação estão girando em torno do eixo vertical sobre a superfície cônica fixa lisa com uma velocidade angular de 4r a d / s . A esfera é mantida na posição b =
Cada uma das quatro esferas de massa m é tratada como uma partícula. As esferas A e B são montadas em uma haste leve e estão inicialmente girando com uma velocidade angular ω 0 em tordo de um eixo ver
O pêndulo simples de massa m e comprimento l é liberado a partir do repouso em θ = 0 . Utilizando apenas o principio do impulso angular e quantidade de movimento, determine a expressão para θ ¨ em ter
Uma pequena partícula de 0,1k g recebe uma velocidade de 2 m / s sobre o plano horizontal x - y e é guiada pela barra curva fixa. O atrito é desprezível. Quando a partícula cruza o eixo y em A , sua v