Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 229

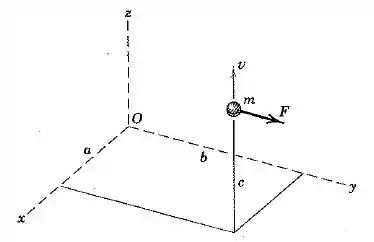
Em um dado instante, a partícula de massa m tem a posição e a velocidade mostradas na figura, e sofre a ação da força F . Determine sua quantidade de movimento angular em torno do ponto O e a taxa de variação no tempo dessa quantidade de movimento angular.

Passo 1

Bom galera, nesse exercício queremos encontrar a quantidade de movimento angular da partícula em torno do ponto especificado para depois encontrar sua taxa de variação no tempo. Pela definição, temos que a quantidade de movimento angular é dada por

H O = r   x   m v

Passo 2

Olhando para a figura, podemos encontrar o valor de r e sabemos que v está na direção k ^ . Dessa forma, substituindo, temos

H O = a i + b j + c k   x   m v k

Realizando o produto vetorial, ficamos com

H O = m v b i - a j

Passo 3

A taxa de variação no tempo da quantidade de movimento angular pode ser dada por

H O ˙ = M O = a i + b j + c k   x   F j ˙

Realizando o produto vetorial, ficamos com

M O = F - c i + a k

Resposta

H O = m v b i - a j

M O = F - c i + a k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força central de atração F sobre um satélite da Terra não pode ter nenhum momento em tordo do centro O da Terra. Para a órbita elíptica específica com eixos maior e menor conforme indicado, um satél
Determine o módulo H 0 da quantidade de movimento angular da esfera de 2k g em torno do ponto O ( a ) usando a definição vetorial da quantidade de movimento angular e ( b ) usando uma abordagem escala
Uma partícula de massa m se desloca com atrito desprezível sobre uma superfície horizontal e está conectada a uma mola leve presa em O . Na posição A a partícula tem a velocidade v A = 4m / s . Determ
A partícula de massa m é suavemente empurrada a partir da posição de equilíbrio A e posteriormente desliza ao longo da trajetória circular lisa que se situa num plano vertical. Determine o módulo da s
A partícula de massa m é lançada a partir do ponto O com uma velocidade horizontal u no instante de tempo t = 0 . Determine sua quantidade de movimento angular H O em relação ao ponto O como uma funçã