Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 48
O pequeno barco a vela pode ser inclinado quando preso às docas, como mostrado, para se realizar reparos abaixo da linha d’água. Uma corda é passada sobre a quilha e presa à doca. Outra corda é presa ao mastro e usada para inclinar o barco. O barco mostrado tem um deslocamento (que é igual à massa total) de , com centro de massa em . O metacentro é o ponto na mediatriz do barco pelo qual passa a resultante vertical das forças de flutuação, e . Calcule a força trativa necessária para manter o barco na posição mostrada.
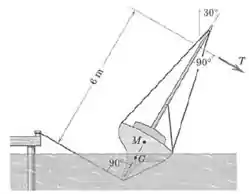
Passo 1
Nosso objetivo é que o barco permaneça em equilíbrio, por isso precisamos fazer algumas exigências:
Ou seja, é preciso que haja equilíbrio de forças e de momentos. Para considerar o equilíbrio das forças vamos olhar para o seguinte desenho:
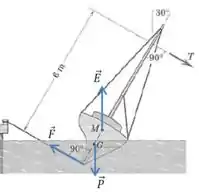
Temos dois pares de forças em direções iguais e sentidos opostos, nesse caso, para que a força resultante seja zero é preciso que haja equilíbrio nas duas direções:
Além disso:
Passo 2
E esses mesmos dois pares de forças com módulos e direções iguais, mas sentidos opostos, formam dois binários, que podemos usar para calcular o momento total.
O par , está separado pela seguinte distância:
E o binário favorece a rotação no sentido anti-horário, então:
Já o par , está separado por outra distância:
E o binário favorece a rotação no sentido horário:
Agora vamos usar a condição de equilíbrio dos momentos:
Resposta
A força trativa necessária é .