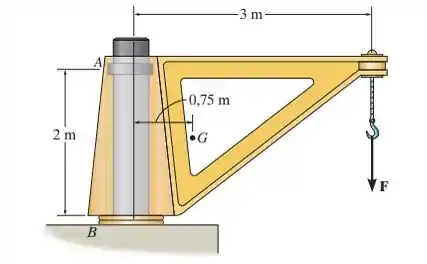
As dimensões de um guindaste, que é fabricado pela Basick Co., são dadas na figura. Se o guindaste tem massa de 800 kg e centro de massa em . O mancal em é radial e apoia somente uma força horizontal, enquanto o mancal em é axial, apoiando componentes horizontal e vertical. Determine a carga máxima que pode ser suspensa a partir de sua extremidade se os mancais selecionados em e puderem suportar uma carga resultante máxima de e , respectivamente.

Vamos começar com a primeira hipótese, que .

Só que temos que tomar um cuidado. Na questão anterior, ao calcularmos a força , percebemos que ela está na direção negativa de ! Portanto, ao continuarmos o cálculo, temos que utilizar o valor correto de , o qual é (na direção negativa).

Desta forma, a carga será:

E com isto, as reações no pino são:

E então, a intensidade da força no pino , temos:

E como , a nossa primeira hipótese é plausível (provavelmente será ela). Vamos só verificar agora que a segunda hipótese é inválida.

Para checarmos a nossa segunda hipótese temos que lembrar que . Desta forma, temos:

Só que nós sabemos que:

Portanto,

Resolvendo a equação acima obtemos:

Só que este valor de força nos dará a seguinte reação no pino : , que é maior (em módulo) que a máxima intensidade no pino , isto é, maior que .

Portanto, a carga máxima foi a da nossa primeira hipótese,

E assim finalizamos a questão!