O pequeno cilindro é fabricado para se deslocar ao longo da haste giratória com um movimento entre e dado por , onde é o tempo contado a partir do instante em que o cilindro passa a posição e é o período de oscilação (tempo para uma oscilação completa). Simultaneamente, a haste gira em torno da vertical na velocidade angular constante . Determine o valor de para o qual a aceleração radial (direção r) é zero.
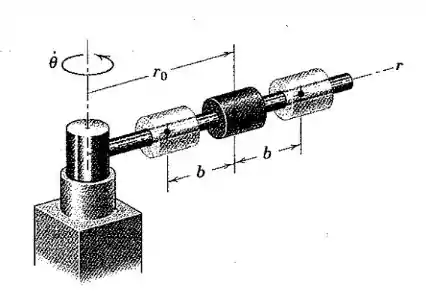
Passo 1
Nosso objetivo é achar o ponto em que a aceleração radial é zero. Como calcular essa aceleração?
Nesse caso vamos ter que considerar duass coisas: o movimento do próprio cilindro entres os pontos e , e a aceleração centrípeta por conta do movimento da haste.
Beleza, já temos tudo para calcular os dois valores!
Passo 2
Para encontrar a aceleração do próprio cilindro é só derivar a função que o enunciado deu em relação ao tempo:
E agora a aceleração centrípeta. Se você esquecer a fórmula para o caso de coordenadas polares, é só lembrar do seguinte:
E o sinal negativo aparece quando nós definimos o sentido positivo como sendo voltado para fora, sendo que a força centrípeta aponta para dentro
Então nossa equação é:
Passo 3
Falta agora encontrar o valor de quando é nulo:
Substituindo com a equação para :
Então:
E então:
Pronto!
Resposta
A aceleração radial é zero quando .