Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 36

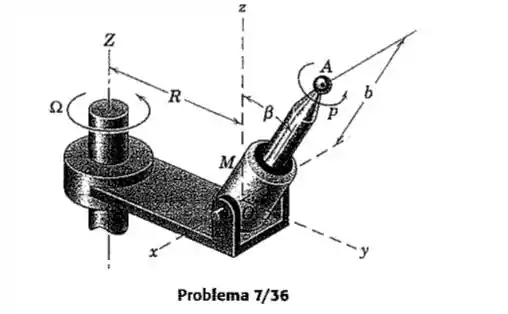
O pequeno motor M é articulado em relação ao eixo x através de O e transmite ao seu eixo AO uma velocidade constante p rad/s no sentido mostrado, em relação á sua carcaça. O conjunto inteiro é, em seguida, colicado para girar em torno do eixo vertical Z na velocidade angular constante Ω rad/s. Simultanneamente, o motor articula em torno do eixo x na taxa constante β ˙ para um intervalo de movimento. Determine a aceleração angular α do eixo AO em termos de β . Expresse seu resultado em termos dos vetores unitários para os eixos om rotação x-y-z.

Passo 1

Para esse problema podemos utilizar a equação 7/7a onde chamando     = ω ⃑

E 7/7a é d       d t X Y Z = d       d t x y z + Ω ⃑ ×       podemos saber a taxa de variação de ω ⃑   nos dois referencias o que gira e o fixo.

Passo 2

Com o auxílio do ângulo β e com a regra da mão direita nós podemos decompor a velocidade angular no eixo x-y-z , que será levando em conta a sua taxa de variação.

ω ⃑ = - β ˙ i ^ + p . s e n β j ^ + p . c o s β + Ω k ^

β ˙ = c o n s t a n t e

Passo 3

Assim nós podemos saber sua taxa variação nós dois referencias utilizando.

d       d t X Y Z = d       d t x y z + Ω ⃑ ×       onde     = ω ⃑

d   ω ⃑ d t X Y Z = d   ω ⃑ d t x y z + Ω ⃑ ×   ω ⃑

d   ω ⃑ d t x y z = d   d t x y z ( - β ˙ i ^ + p . s e n β j ^ + p . c o s β + Ω k ) ^

= 0 + ( p β ˙ cos ⁡ β j ^ - p β ˙ s e n β k ^

= ( p β ˙ cos ⁡ β j ^ - p β ˙ s e n β k ^ )

Ω ⃑ ×   ω ⃑ = Ω k ^ × - β ˙ i ^ + p . s e n β j ^ + p . c o s β + Ω k ^ =

= - Ω . β ˙ j ^ - Ω . p . s e n β i ^

d   ω ⃑ d t X Y Z = d   ω ⃑ d t x y z + Ω ⃑ ×   ω ⃑ = p β ˙ cos ⁡ β j ^ - p β ˙ s e n β k ^ - Ω . β ˙ j ^ - Ω . p . s e n β i ^

α ⃑ = - Ω . p . s e n β i ^ + β ˙ p c o s β - Ω j ^ - p β ˙ s e n β k ^

Resposta

α ⃑ = - Ω . p . s e n β i ^ + β ˙ p c o s β - Ω j ^ - p β ˙ s e n β k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pêndulo consiste de uma placa tendo uma massa de 6kg e uma barra fina tendo uma massa de 2kg. Determine o raio de giração do pêndulo em relação a um eixo perpendicular à página e passando pelo ponto
O pêndulo consiste da barra fina de 3kg e a placa fina de 5kg. Determine a localização y - do centro de massa G do pêngulo; em seguida, calcule o momento de inércia do pêndulo em relação a um eixo per
Determine o momento de inércia da massa da placa fina em relação a um eixo perpendicular à página e passando pelo ponto O . O material tem uma massa por unidade de área de 20kg/m2.
Determine o momento de inércia da manivela suspensa em relação ao eixo x . O material é aço para o qual a densidade é ρ = 7,85 Mg/m3.
Cada uma das três barras finas tem uma massa m . Determine o momento de inércia da montagem em relação a um eixo que é perpendicular à página e passa pelo ponto central O .