A roda tem uma massa de 50 kg com um raio de giração de 250 mm em relação ao seu centro e é mantida inicialmente em repouso sobre o bloco inclinado de 25 kg. A roda é liberada quando uma força é aplicada ao bloco. Calcule a aceleração do bloco, a aceleração do centro da roda, e o valor mínimo do coeficiente de atrito estático para o qual não ocorrerá nenhum deslizamento entre a roda e o bloco.
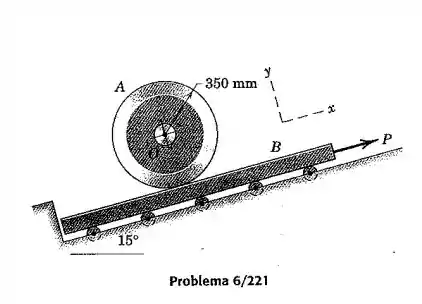
Passo 1
Para resolvermos esse problema vamos usar os conceitos de aceleração relativa e somatória de forças para encontrarmos o coeficiente de atrito do sistema. Vamos dividir o sistema em dois subsistemas: a roda e o bloco.
Passo 2
Vamos começar calculando para o bloco. Temos que a somatória das forças será
Onde é a aceleração do bloco. Agora vamos calcular para a roda. Nesse caso teremos que calcular para o movimento de translação e de rotação, fazendo assim a somatória das forças e dos torques. Temos então que
Onde é a velocidade do disco. Vamos analisar agora as equações para o caso giratório do disco. Temos pela somatória de torques que
Se analisarmos agora a aceleração relativa dos dois sistemas, vamos ter que , logo
Com um auxílio de um programa para resolver sistemas, chegaremos que as acelerações serão
No sentindo positivo de x
No sentido negativo de x
Resposta
No sentindo positivo de x
No sentido negativo de x