Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 38

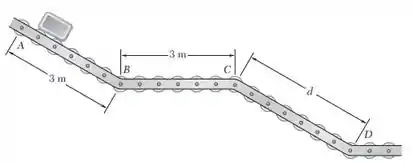
Um pequeno pacote é liberado do repouso em A e move ao longo do transportador de rolete ABCD. O pacote tem uma aceleração uniforme de 4,8   m / s ² enquanto se move para baixo pelas seções AB e CD, com velocidade constante entre B e C. Se a velocidade do pacote em D é 7,2   m / s , determine (a) a distância dentre C e D, (b) o tempo requerido para o pacote alcançar D.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente encontre a distância dentre C e D, (b) o tempo requerido para o pacote alcançar D.

  1. Para A → B

    2. E C → D

    Temos: v 2 = v 0 2 + 2 a   x   x - x 0

    Então

    Em B: v B C 2 = 0 + 2   x   ( 4,8 m / s ² )   x   3 - 0 m

    = 28,8 m ¹ / s ² ( v B C = 5,3666 m / s )

    E em D: v D 2 = v B C 2 + 2 a C D   x   ( x D - x C ) d = x d - x C

    Ou ( 7,2 m / s ) ² = ( 28,8 m 2 / s ² ) + 2   x   ( 4,8 m / s ² ) d

    Passo 2

  2. Para A → B

E C → D

Temos: v = v 0 + a t

Então A → B

5,3666 m / s = 0 + ( 4,8 m / s ² ) t A B

t A B = 1,11804 s

Em C → D : 7,2 m / s = 5,3666 m / s + ( 4,8 m / s ² ) t C D

Ou t C D = 0,38196 s

Agora,

Para B → C ,

Temos: x C = x B + v B C t B C

Ou t B C = 0,55901 s

Finalmente, t D = t A B + t B C + t C D = 1,11804 + 0,55901 + 0,38196 s

Resposta

  1. d = 2,40 m
  2. t D = 2,06 s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que r ˙ = h ϕ ˙ sen θ sabendo que, para o instante mostrado na figura, o degrau AB do aparelho de ginástica está girando no sentido anti-horário a uma taxa constante ϕ ˙ .
Para a hélice cônica do Problema 11.95, determine o ângulo que o plano de oscilação forma com o eixo y.
O movimento de uma partícula sobre a superfície de um cilindro circular reto é definido pelas relações R = A, 2 π t e z = At2/4, onde A é uma constante. Determine as intensidades da velocidade e da ac
O movimento tridimensional de uma partícula é definido por suas coordenadas cilíndricas (veja a Fig. 11.26) R = A/(t + 1), θ = Bt e z = Ct/(t + 1). Determine as intensidades da velocidade e da acelera
Como o motorista de um automóvel viaja para o norte a 25 km/h em um estacionamento, ele observa um caminhão aproximando pelo noroeste. Depois ele reduz sua velocidade escalar para 15 km/h e assim que