Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 94
Pequenos roletes sobre rolamentos montados nas extremidades da barra esbelta de massa e comprimento limitam o movimento da barra nas ranhuras horizontais -. Se um momento é aplicado à barra, inicialmente em repouso em , determine as forças exercidas sobre os roletes em e , quando a barra começa a se mover.
Passo 1
Vamos começar procurando a aceleração angular do sistema. Para isso precisamos montar uma equação de momentos:
Onde é um ponto de referência que precisamos escolher. Qual é a melhor opção para esse caso?
Bom, nós não conhecemos as forças em e ainda, então seria uma boa ideia escolher um ponto que anule essas duas forças:
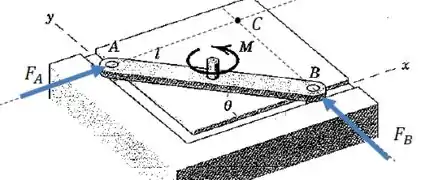
Quando desenhamos as linhas de ação das forças, fica claro que o ponto cumpre essa função.
Passo 2
Então vamos desenvolver aquela equação:
O único momento (em relação ao ponto ) que sobrevive à nossa escolha será o momento que age no centro da barra:
O momento de inércia em relação ao centro de massa da barra é:
E se considerarmos que a aceleração de em relação a (ou vice-versa) é , a aceleração do centro de massa que fica exatamente no meio do caminho entre os dois pontos será:
E o centro de massa está a uma distância perpendicular do ponto (metade do lado do quadrado). Então:
Passo 3
Agora vamos aplicar a segunda lei de Newton nas duas direções. Antes, é interessante incluir a aceleração do centro de massa no nosso desenho:
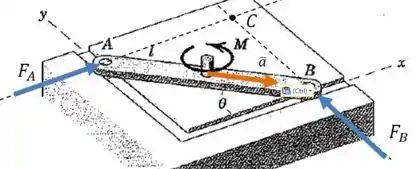
O ângulo vale no instante que estamos estudando. Começamos pela direção horizontal:
Que também podemos representar em forma vetorial, de acordo com o nosso desenho:
E agora a direção vertical:
E o sinal negativo indica que o verdadeiro sentido da força é contrário ao que nós representamos no desenho, então sua representação vetorial é:
Resposta
As forças são e .