O haste esbelta de massa e comprimento é liberada a partir do repouso na posição vertical com o pequeno rolete na extremidade apoiado sobre o plano inclinado. Determine a aceleração inicial de .
Passo 1
Vamos começar fazendo um esquema das forças externas que agem sobre a haste:
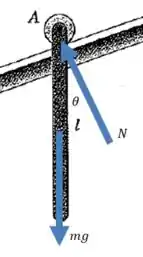
Vamos começar escrevendo uma equação de momentos em relação ao ponto . Quando escolhemos esse ponto, o momento das duas forças ( e ) são nulos, porque as linhas de ação de ambas cruzam o ponto .
Então:
O momento de inércia da haste em relação a um eixo que passa pelo seu centro de massa é:
E para escrever o segundo termo da equação vamos precisar de uma análise mais cuidadosa.
Passo 2
Conforme a haste desce pelo plano inclinado, o seu centro de massa adquire certas acelerações.
A primeira é a aceleração que queremos calcular, associada à translação do centro de massa, que aponta no sentido que desce o plano inclinado.
A segunda é a aceleração associada à rotação do centro de massa em torno do ponto , que aponta na direção tangencial à trajetória:
Onde é a distância entre o ponto e o centro de massa.
Então o nosso somatório fica da seguinte forma:
E nesse último termo surge o porque é a distância perpendicular entre o centro de massa e a linha de ação da aceleração , que é inclinada em relação à horizontal por um ângulo .
Juntando todas essas informações:
Podemos dividir tudo por para simplificar, e depois multiplicar por :
Ok, essa é nossa primeira equação. Como temos duas variáveis desconhecidas ( e ), precisamos de mais uma equação para poder resolver o problema.
Passo 3
Vamos usar a segunda lei de Newton para obter nossa segunda equação.
Onde é a direção paralela ao plano inclinado (não é a horizontal!).
A única força que age nessa força é uma componente da força peso:
A aceleração de translação é paralela à essa direção, e a aceleração de rotação em torno de aponta (no momento do desenho) na direção horizontal para a esquerda, que forma um ângulo com a nosa direção , ou seja:
Então:
Passo 4
Agora ficamos com um sistema de duas equações:
Vamos isolar na equação de baixo:
E substituir isso na equação de cima:
E então:
Resposta
A aceleração inicial é .