Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 26

A viga de madeira, montada como indicado, é submetida a uma força cortante vertical de 5kN. Sabendo-se que o espaçamento longitudinal dos pregos é s= 35mm e que cada prego tem 65mm de comprimento, determinar a força cisalhante em cada prego.

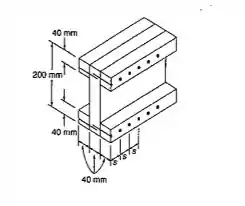
Passo 1

Primeiro a gente precisa calcular o momento de inércia da peça.

Vamos desenhar a seção de frente pra facilitar o cálculo do momento de inércia.

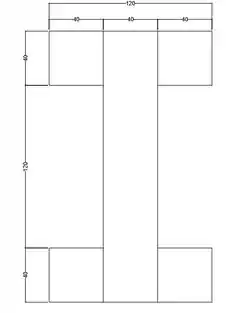
Separando em 5 partes, sendo o maior retângulo a única peça diferente teremos:

I 1 = 40 × 200 ³ 12 = 26,667 × 10 6 m m 4

Para os quadrados das bordas teremos que usar o teorema dos eixos paralelos, a distância do centro da peça até o centro dos quadrados é:

d = 120 2 + 40 2 = 80 m m

O teorema diz que:

I = I 2 + A d ²

Calculando I 2 :

I 2 = 40 × 40 3 12 = 213,333 × 10 3 m m 4

Enfim:

I = 213,333 × 10 3 + 40 × 40 × 80 2 = 10,453 × 10 6 m m 4

E como temos 4 quadradinhos precisamos multiplicar I por 4 para obter a inércia de todas essas peças, dessa forma a inércia final será:

I p e ç a = I 1 + 4 I = 68,479 × 10 6 m m 4

Passo 2

Agora a gente vai calcular o fluxo de cisalhamento da ligação e pra isso nós precisamos do momento estático de cada peça que é ligada a central.

Q = ∑ y - A = 80 × 40 × 40 = 128000 m m ³

Assim o fluxo de cisalhamento será:

q = V Q I p e ç a = 5000 × 128 × 10 3 68,470 × 10 6 = 9,35 N / m m

Por fim a força em cada prego será o fluxo multiplicado pelo espaçamento:

F = q s = 9,35 × 35 = 327,25 N

Resposta

F = 327,25 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga mostrada na figura suporta uma força concentrada P e seu centro. Se for feita de uma chapa com largura constante b , determine a tensão de flexão máxima absoluta na viga
A viga com avanço foi construída com duas peças de madeira de 50 mm por 100 mm escoradas como mostra a figura. Se a tensão de flexão admissível for σ a d m = 4,2M P a , determine a maior carga P que p
Determine a variação do raio r da viga em balanço que suporta a carga distribuída uniforme, de modo que ela tenha uma tensão de flexão máxima constante σ m á x á em todo o seu comprimento.
A viga tem largura w e altura que varia como mostra a figura. Se ela suportar uma força concentrada P em sua extremidade, determine a tensão de flexão máxima absoluta na viga e especifique sua localiz
A viga tem a forma de um tronco de cone reto com diâmetro de 12 mm em A e de 300 mm em B. Se ela suportar uma força de 750 N em A, determine a tensão de flexão máxima absoluta na viga e especifique su