Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 116

O perfil mostrado é formado pela flexão de uma placa fina de aço. Considerando que a espessura t é pequena quando comparada ao comprimento a dos lados do perfil, determine a tensão:

  1. No ponto A
  2. No ponto B
  3. No ponto C

Passo 1

Fala galerinha, nosso objetivo é determinar a tensão nos pontos A, B e C, certo?

Para isso precisamos lembrar que a nossa fórmula de tensão é dada por.

σ x = P A - M y I

E antes de calcularmos os termos dela, precisamos fazer uma transformação na nossa seção, essa transformação vai facilitar e muito o nosso cálculo, assim, teremos que:

E porque temos que fazer essas modificações? Porque vamos trocar essa seção muito complicada, por essa aqui oh, olha que maravilha:

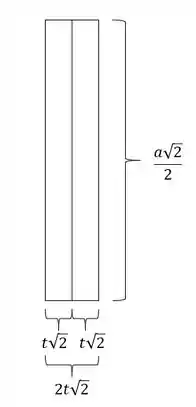
Ou seja, ficamos com uma seção retangular que sabemos trabalhar, e com isso podemos definir pontos e carregamentos.

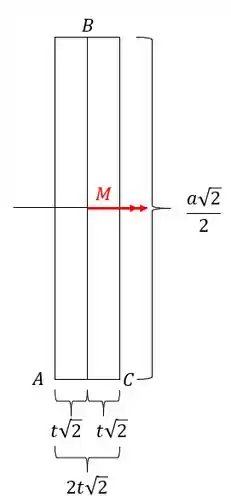
E esse momento é dado por:

M = - P e = - P a 2 2 2 = - P a 2 4

Passo 2

Vamos definir o momento de inércia, a área e y, assim teremos que:

  • I

    • I = b h 3 12 = 2 t 2 × a 2 2 3 12 = 2 t 2 12 × a 3 2 2 8

    I = t a 3 12

  • Área da seção

    • A = 2 t 2 a 2 2 = 2 a t

  • y - positivo e negativo

Substituindo na nossa equação temos que:

σ = P A - M y I

σ A = σ C = P 2 a t - - P a 2 4 - a 2 4 t a 3 12

σ A = σ C = P 2 a t - 12 P a 2 2 16 t a 3

σ A = σ C = P 2 a t - 24 P 16 t a

σ A = σ C = P 2 a t - 3 P 2 a t

σ A = σ C = - 2 P 2 a t = - P a t

E para o ponto B tem-se que:

σ = P A - M y I

σ B = P 2 a t - - P a 2 4 a 2 4 t a 3 12

σ B = P 2 a t + 12 P a 2 2 16 t a 3

σ B = P 2 a t + 24 P 16 t a

σ B = P 2 a t + 3 P 2 a t

σ B = 4 P 2 a t = 2 P a t

Resposta

  1. σ A = - P a t

  2. σ B = 2 P a t

  3. σ C = - P a t
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga-cmxao está sujeita a um momento fletor M = 25 kN · m direcionado, como mostra a figura. Determine a tensão de flexão máxima na viga e a orientação do eixo neutro.
Determine o valor máximo do momento fletor M de modo que a tensão de flexão no elemento não ultrapasse 100M P a .
O momento interno resultante que age na seção transversal da escora de alumínio tem valor M = 520N · m e está direcionado como mostra a figura. Determine a tensão de flexão máxima na escora. A localiz
A viga tem seção transversal retangular. Se estiver sujeita a um momento fletor M=3.500N . m direcionado como mostra a figura, determine a tensão de flexão máxima na viga e a orientação do eixo neutro
Se o momento interno resultante que age na seção transversal da escora de alumínio tiver valor M = 520 N.m e for direcionado como mostra a figura, determine a tensão de flexão nos pontos A e B. A loca