Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 173
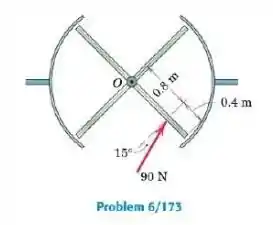
Uma pessoa que passa através da porta giratória exerce uma força horizontal de em um dos quatro painéis da porta e mantém o ângulo de 15° constante em relação a uma linha que é normal ao painel. Se cada painel é modelado por uma placa retangular uniforme de que possui de comprimento quando visto de cima, determine a velocidade angular final da porta se a pessoa exerce a força por três segundos. A porta está inicialmente em repouso e o atrito pode ser desprezado.
Passo 1
A equação da quantidade de movimento angular em relação a um ponto fixo é dada por
Passo 2
Substituindo os valores fornecidos pela questão na equação anterior, temos
Simplificando e resolvendo para , achamos
Resposta
Exercícios de Livros Relacionados
O rotor de um motor elétrico tem uma velocidade angular de 3.600 rpm quando a carga e a potência são cortadas. O rotor de 50 kg, com um raio de giração centroidal de 180 mm, chega então ao estado de r
O rotor de um motor elétrico tem massa de 25 kg e raio de giração de 180 mm. Observa-se que são necessários 4,2 min para o rotor chegar ao repouso a partir de uma velocidade angular de 3.600 rpm após
Um cilindro de 240 mm de raio e massa de 8 kg repousa sobre um transportador de 3 kg. O sistema está em estado de repouso quando uma força P de intensidade 10 N é aplicada como mostrado na figura dura
Um cilindro de 240 mm de raio e massa de 8 kg repousa sobre um transportador de 3 kg. O sistema está em estado de repouso quando uma força P de intensidade 10 N é aplicada como mostrado na figura dura
No arranjo das engrenagens mostrado na figura, as engrenagens A e C estão presas à barra ABC, que é livre para girar em torno de B, enquanto a engrenagem interna B é fixa. Sabendo que o sistema está e