Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.3 - Ex. 63

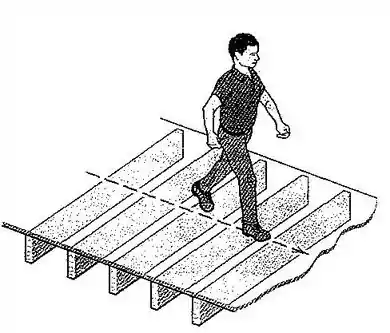
63. Quando uma pessoa está posicionada no centro do assoalho mostrado, ela provoca uma deflexão estática do piso sob seus pés. Se ela anda (ou corre!) na mesma área, quantos passos por segundo levaria o piso para vibrar com a máxima amplitude vertical?

Passo 1

Bom, para começar, a gente tem que perceber que a força peso será equivalente à uma “força elástica” causada:

Onde é um equivalente à constante elástica e é a variação do vertical do piso, ou seja, a deflexão.

Isolando :

Passo 2

Agora, vamos utilizar a fórmula de cálculo da frequência de ressonância:

Como já temos , podemos substituir na fórmula:

Passo 3

Para uma reação máxima, temos que:

E a frequência será:

Resposta

A quantidade de passos por segundo para a pessoa fazer com que o piso vibre com máxima amplitude vertical é dada pela frequência:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando uma lata de 20N é pendurada na extremidade inferior de uma mola vertical, a mola sofre uma distensão de 20c m . (a) Qual é a constante elástica da mola? (b) A mesma mola é colocada horizontalme

São pendurados em uma viga horizontal nove pêndulos com os seguintes comprimentos: (a) 0,10 ; (b) 0,30 ; (c) 0,40 ; (d) 0,80 ; (e) 1,2 ; (f) 2,8 ; (g) 3,5 ; (h) 5,0 ; (i) 6,2 m . A viga sofre oscilaçõ

Um bloco de 2,00 k g está pendurado em uma mola. Quando um corpo e 300 g é pendurado no bloco, a mola sofre uma distensão adicional de 2,00 c m . (a) Qual é a constante elástica da mola? (b) Determine

Um objeto executa um movimento harmônico simples com período de 0,300 s e amplitude igual a 6,00 cm. Em t = O, o objeto está instantaneamente em repouso em x = 6,00 cm. Calcule o tempo que o objeto le

Um bloco de massa igual a 0,200 kg está submetido a uma força restauradora elástica e a constante da força é igual a 10,0 N/m. (a) Faça um gráfico da energia potencial elástica U em função do deslocam