50. O carrinho de é acionado pela força harmônico mostrada na figura. Se , determine a faixa das frequências de excitação para a qual o módulo da resposta em regime permanece é inferior a .
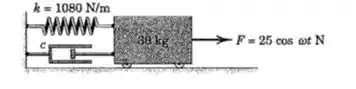
Passo 1
Bom, primeiro a gente vai lembrar a fórmula da frequência natural do sistema, que é dada por:
Onde é a constante de mola e a massa do carrinho.
Passo 2
Agora, vamos lembrar a fórmula da amplitude :
Onde é o valor da força de excitação inicial e a frequência que a gente quer:
Passo 3
Como temos a fórmula da frequência angular em função da amplitude do regime, vamos aplicar o módulo do valor máximo que queremos de amplitude (módulo porque a amplitude pode variar de até ) e encontrar o valor das frequências que queremos:
Vamos então substituir esses dois valores na fórmula da frequência que obtivemos no final do , para só depois ver as condições em que vão estar nossa desigualdade
Para , temos que:
Agora para :
Pronto! Esses valores são os que iremos usar em nossa desigualdade. Porém, resta a dúvida em relação a que intervalos devemos usar? Se for prestar bem atenção, ao calcularmos o valor da amplitude para alguma frequência entre e , vamos ver que ela será superior a , quer ver só:
Peguemos :
Agora, peguemos um valor maior do que , por exemplo :
Viu só! Com isso, temos que os valores que a frequência angular pode assumir para a amplitude não ser superior a são
Resposta
Os valores que a frequência angular pode assumir para a amplitude não ser superior a são: