Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 36
36. Para o sistema massa-mola amortecido mostrado, determine o coeficiente de amortecimento viscoso para o qual ocorrerá um amortecimento crítico
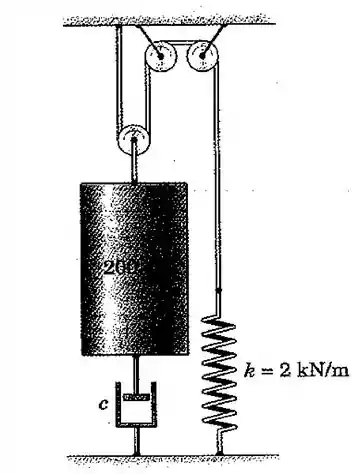
Passo 1
Vamos fazer a representação esquemáticas das forças que estão agindo na polia que sustenta o nosso bloco de :
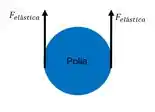
Como o bloco está sujeito a ação da polia, que por sua vez tem o dobro da força elástica provocada pela mola, já temos que o nosso sisteminha de interesse, experimenta uma constante elástica de , considerado é claro, como a constante da mola, de .
Só que tem uma mágica por trás dessa questão. A nossa polia acima, se você observar bem, a corda que por ela passa, irá percorrer o dobro de distância do que as demais polias.
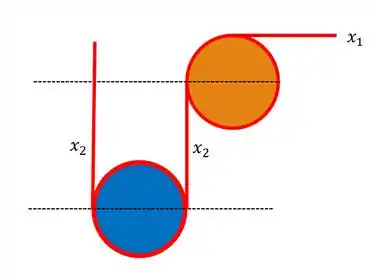
Ou seja, se nossa polia estava sujeita a uma força de vezes o deslocamento, e agora já sabemos que o deslocamento experimentado é de , é como se a força total que o bloco vai experimentar fosse dada por , ou seja:
E a nossa constante equivalente, é de :
Passo 2
Se já Temos a constante equivalente do nosso sisteminha, igual a e a massa do bloco. O que isso quer dizer?
Ora bolas, quer dizer que já podemos determinar a frequência angular natural do nosso sistema, a qual é dada pela relação abaixo:
Substituindo os valores numéricos adequados, chegamos ao seguinte valor:
Passo 3
Obtida a frequência natural do sistema, basta agora utilizar a condição para que ocorra amortecimento crítico. Não lembra! Vou refrescar sua memória!
Ocorre amortecimento crítico em um sistema, quando o seu fator de amortecimento , é exatamente igual a
E para nossa alegria o fator de amortecimento está relacionado ao coeficiente de amortecimento viscoso pela seguinte fórmula:
Sabendo que e conhecendo os valores da outras variáveis, alcançamos nosso resultado: