Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 170

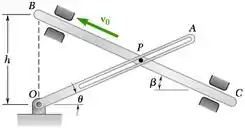
O pino P está ligado a haste BC e desliza livremente ao longo da ranhura existente na haste AO. Determine a taxa de variação θ ˙ do ângulo θ , sabendo que BC se move com velocidade escalar constante v0. Expresse sua resposta em termos de v0, h, β e θ .

Passo 1

E ai gurizada tudo certinho? determine a taxa de variação θ ˙ do ângulo θ , sabendo que BC se move com velocidade escalar constante v0. Expresse sua resposta em termos de v0, h, β e θ .

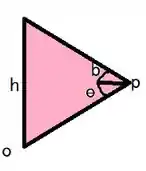
Do diagrama

r sin ⁡ 90 ° - β = h sin ⁡ β + θ

ou

r sin ⁡ β cos ⁡ θ + cos ⁡ β sin ⁡ θ = h cos ⁡ β

ou

r = h tan ⁡ β cos ⁡ θ + sin ⁡ θ

Além disso,

v θ = v 0 sin ⁡ β + θ             o n d e             v θ = r θ ˙

Então

h θ ˙ tan ⁡ β cos ⁡ θ + sin ⁡ θ = v 0 sin ⁡ β cos ⁡ θ + cos ⁡ β sin ⁡ θ

Passo 2

Solução alternativa.

r = h tan ⁡ β cos ⁡ θ + sin ⁡ θ

r ˙ = h tan ⁡ β sin ⁡ θ - cos ⁡ θ ( tan ⁡ β cos ⁡ θ + sin ⁡ θ ) 2

Agora

v 0 2 = v r 2 + v 0 2 = ( r ˙ ) 2 + ( r θ ˙ ) 2

v 0 2 = h θ ˙ tan ⁡ β sin ⁡ θ - cos ⁡ θ ( tan ⁡ β cos ⁡ θ + sin ⁡ θ ) 2 2

+ h θ ˙ tan ⁡ β cos ⁡ θ + sin ⁡ θ

ou

v 0 = ± h θ ˙ tan ⁡ β cos ⁡ θ + sin ⁡ θ

+ ( tan ⁡ β sin ⁡ θ - cos ⁡ θ ) 2 ( tan ⁡ β cos ⁡ θ + sin ⁡ θ ) 2 + 1 1 / 2

= ± h θ ˙ tan ⁡ β cos ⁡ θ + sin ⁡ θ tan 2   β + 1 ( tan ⁡ β cos ⁡ θ + sin ⁡ θ ) 2 1 / 2

Observe que à medida que o aumenta, o membro BC se move na direção indicada. Assim, a raiz positiva é escolhida.

Resposta

θ ˙ = v 0 cos ⁡ β h ( tan ⁡ β cos ⁡ θ + sin ⁡ θ ) 2

θ ˙ = v 0 cos ⁡ β h ( tan ⁡ β cos ⁡ θ + sin ⁡ θ ) 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro está descendo a encosta de inclinação θ 1 com os freios ligeiramente acionados de modo que a velocidade v é constante. A inclinação diminui bruscamente para θ 2 no ponto A . Se o condutor não
Um trem de brinquedo possui acoplamentos magnéticos cuja força de atração máxima é 0,9N entre carros adjacentes. Qual é a força máxima P com a qual uma criança pode puxar a locomotiva e não romper o t
Determine a tração P no cabo que dará ao bloco de 50k g uma aceleração constante de 2m / s 2 para cima no plano inclinado.
O avião comercial a jato A com 340t possui quatro motores, cada um dos quais produz um empuxo quase constante de 200k N durante a decolagem. Uma pequena aeronave B taxia em direção à extremidade da pi
Um pequeno pacote é depositado pela correia transportadora em uma rampa com 30 ° em A com uma velocidade de 0,8m / s . Calcule a distância s sobre a superfície plana B C na qual o pacote atinge o repo