Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 35
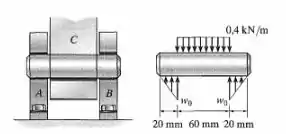
O pino liso está apoiado em duas chapas e e sujeito a uma carga de compressão de provocada pela barra . Determine a intensidade da carga distribuída das chapas agindo sobre o pino e represente graficamente os diagramas de força cortante e momento fletor para o pino.
Passo 1
Falaa! Essa é uma questão de desenhar diagramas. Só seguir esse passo a passo aque a gente vai fazer que dá bom!
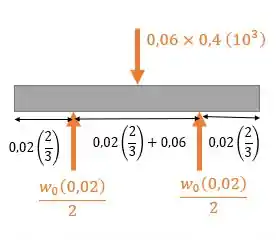
A gente precisa achar . Vamos transformar essas cargas distribuídas ali embaixo por cargas pontuais distantes dois terços da borda do triângulo. E a de cima, fica uma carga no meio.
Passo 2
Vamos dividir nossa viga em seções. Nossos pontos críticos serão onde começa e onde termina nossos carregamentos distribuídos. Teremos então três seções.
Para cada intervalo, a gente corta a viga numa seção genérica, distanciada da origem estabelecida por nós mesmos.
O próximo passo é achar as equações do cortante e do momento para as diferentes seções. Aí é colocar as representações dos esforços com convenção positiva dentro da nossa seção e usar as equações de equilíbrio para achar os valores desses esforços.
Só uma observação: aqui a gente volta a usar o carregamento como distribuído, tá?
Seção 1:
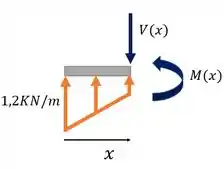
Aqui nossa origem está em . Nós cortamos a viga nesse intervalo, posiocionamos as componentes positivas dos esforços e olhamos só para a parte da viga à esquerda dessa seção.
Percebe que a gente precisa determinar a parte mais baixa desse trapézio do carregamento. Vamos usar semelhança de triângulos.
Agora a gente calcula nossas coisinhas dividindo esse trapézio em um triângulo e um retângulo:
Fazemos o somatório de momentos na nossa seção
Passo 3
Fazemos o mesmo para a segunda seção:
Seção 2:
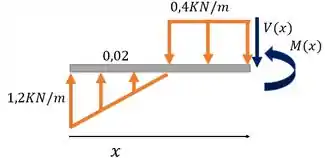
Passo 4
Fazemos o mesmo para a segunda seção:
Seção 2:
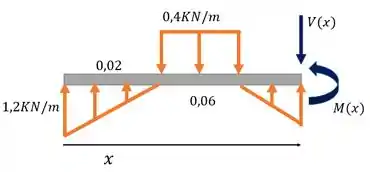
De novo, precisamos achar a altura daquel triângulo ali
Passo 5
Achamos as equações! Aí a gente esboça os diagramas!
Às vezes as equações ficam feias, mas para esboçar, você pode achar alguns pontos chave (onde as curvas cortam os eixos coordenados e nos extremos das seções), os valores máximos e mínimos, e se ligar no tipo de curva que precisa fazer.
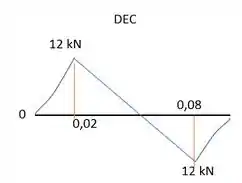
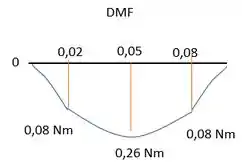
Utilizando as equações podemos traçar os gráficos:
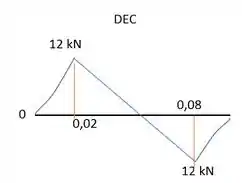
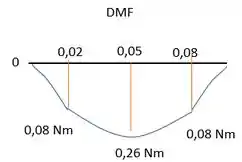
Resposta
