Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 32
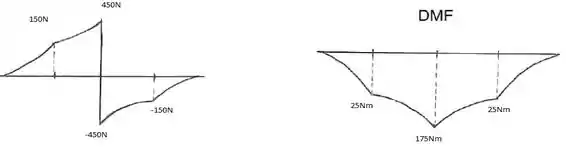
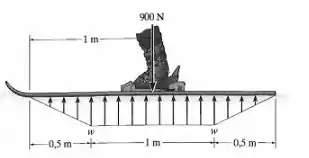
O esqui suporta o peso de do homem. Se a carga de neve em sua superfície inferior for trapezoidal, como mostra a figura, determine a intensidade e, então, represente graficamente os diagramas de força cortante e momento fletor para o esqui.
Passo 1
Primeiramente, podemos determinar utilizando as equações de equilíbrio. Vamos desenhar o DCL com as forças resultantes de cada carregamento distribuído:
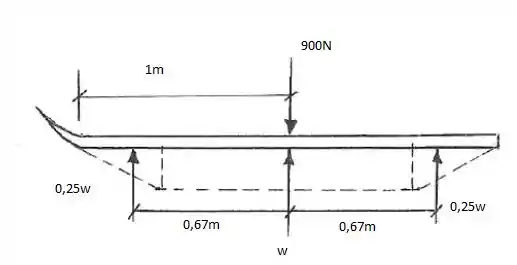
Passo 2
Dado o valor de w, podemos fazer os diagramas de cortante e de momento fletor, respectivamente:
Resposta
Exercícios de Livros Relacionados
Determine as cargas internas resultantes que agem na seção transversal que passa pelos pontos C e D da viga no Problema 1.15.
Determine a resultante das forças internas normal e de cisalhamento no elemento em: ( a ) seção a - a e ( b ) seção b - b , sendo que cada uma delas passa pelo ponto A . Considere θ=60 ° . A carga de
Determine as cargas internas resultantes que agem sobre: ( a ) seção a - a e ( b ) seção b - b . Cada seção está localizada no centroide, ponto C .
A viga suporta a carga distribuída mostrada. Determine as cargas internas resultantes nas seções transversais que passam pelos pontos D e E. Considere que as reações nos apoios A e B sejam verticais.
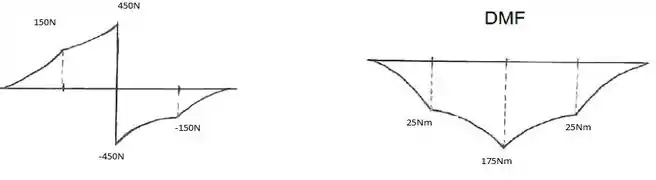
A força F = 400 N age no dente da engrenagem. Determine as cargas internas resultantes na raiz do dente, isto é, no centroide da seção a-a (ponto A).