Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 24
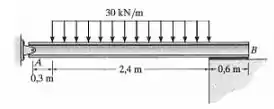
A viga está parafusada ou presa por pino em e repousa sobre um coxim em que exerce uma carga uniformemente distribuída na viga ao longo de seu de comprimento. Represente graficamente os diagramas de força cortante e momento fletor para a viga se ela suportar uma carga uniforme de .
Passo 1
Falaaa galerinha bonita, tudo beleza?!
Esse exercício aqui nos diz que a viga está parafusada em e repousa sobre um coxim em que exerce uma carga uniformemente distribuída na viga ao longo de seu de comprimento. E sabendo que a viga deve suportar uma carga de .
Belezoca, primeiro a gente faz o . Devido à força uniformemente distribuída ali no final, teremos a seguinte situação:
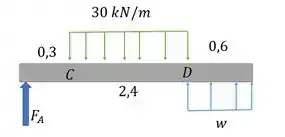
Podemos calcular e pelas equações de equilíbrio:
Logo:
E para :
Passo 2
Vamos achar as equações do cortante e do momento para as diferentes seções. Aí é colocar as representações dos esforços com convenção positiva dentro da nossa seção e usar as equações de equilíbrio.
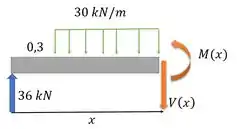
Seção AC:
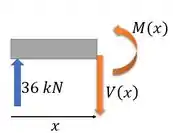
Aí a gente esquece o resto da viga à direita, e foca só nessa parte. Fica assim:
Logo:
E o somatório de momentos em relação a extremidade direita fica desse jeito:
Passo 3
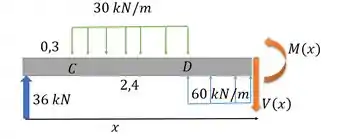
Seção CD:
Aí a gente esquece o resto da viga à direita, e foca só nessa parte. Fica assim:
E o somatório de momentos em relação a extremidade direita desse desenhinho:
Passo 4
Seção DB:
Passo 5
As equações de esforços internos são:
Às vezes as equações ficam feias, mas para esboçar, você pode achar alguns pontos chave (onde as curvas cortam os eixos coordenados e nos extremos das seções), os valores máximos e mínimos, e se ligar no tipo de curva que precisa fazer.
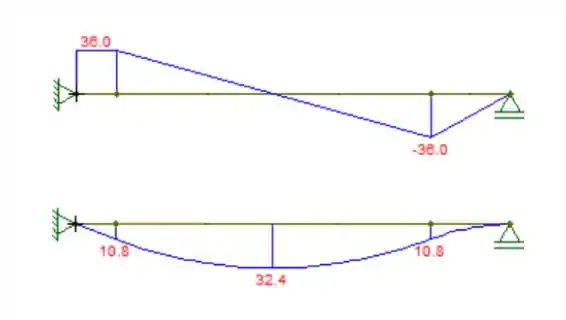
Utilizando as equações podemos traçar os gráficos:
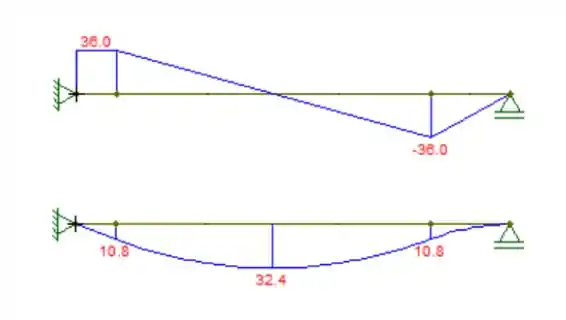
Resposta
