Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 20

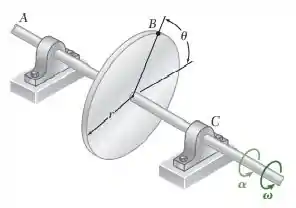
Uma placa circular de raio 250   m m mostrada na figura está inicialmente em repouso e tem a aceleração angular definida pela relação α = α 0 cos ⁡ ( π t / T ) . Sabendo que T = 1,5   s e α 0 = 10   r a d   / s 2 , determine a intensidade da aceleração total do ponto B quando a t = 0 , b t = 0,5   s , c t = 0,75   s .

Passo 1

Fala aí, galerinha. Tudo certo? Bora para mais uma questãozinha de Dinâmica. Neste problema temos que determinar a intensidade da aceleração total do ponto B em diferentes instantes.

Para isso, vamos utilizar a relação de aceleração angular para um movimento circular uniformemente acelerado:

α = d ω d t = α 0 cos ⁡ π t T  

Integrando os dois lados da equação, temos:

∫ 0 ω d ω = ∫ 0 t α 0 cos ⁡ π t T   d t ω = α 0 T π sin ⁡ π T - e - t 0 t ω = α 0 T π sin ⁡ π t T

Sabemos que a aceleração tangencial é dada por:

a t = r α = r α 0 cos ⁡ π t T a t = 0,25 10 cos ⁡ π t 1,5 a t = 2,5 cos ⁡ π t 1,5

E para a aceleração normal, temos:

a n = r ω 2 = r α 0 2 T 2 π sin 2 ⁡ π t T a n = 5,70 sin 2 ⁡ π t 1,5

Com isso, a aceleração total vai ser:

a B 2 = a t 2 + a n 2 a B 2 = 2,5 cos ⁡ π t 1,5 2 + 5,70 sin 2 ⁡ π t 1,5 2

Passo 2

Agora que a gente determinou uma equação para a aceleração no ponto B em função do tempo, podemos encontrar as acelerações nos instantes pedidos. Para t = 0 , temos:

a B 2 = 2,5 cos ⁡ π t 1,5 2 + 5,70 sin 2 ⁡ π t 1,5 2 a B 2 = 2,5 cos ⁡ π ∙ 0 1,5 2 + 5,70 sin 2 ⁡ π ∙ 0 1,5 2 a B = 2,50   m / s 2

Para t = 0,5   s :

a B 2 = 2,5 cos ⁡ π t 1,5 2 + 5,70 sin 2 ⁡ π t 1,5 2 a B 2 = 2,5 cos ⁡ π ∙ 0 , 5 1,5 2 + 5,70 sin 2 ⁡ π ∙ 0 , 5 1,5 2 a B = 4,45   m / s 2

E para t = 0,75   s , temos:

a B 2 = 2,5 cos ⁡ π t 1,5 2 + 5,70 sin 2 ⁡ π t 1,5 2 a B 2 = 2,5 cos ⁡ π ∙ 0 , 7 5 1,5 2 + 5,70 sin 2 ⁡ π ∙ 0 , 7 5 1,5 2 a B = 5,70   m / s 2

É isso, galerinha. Bora praticar mais pra ficar craque!

Resposta

a B = 2,50   m / s 2

a B = 4,45   m / s 2

a B = 5,70   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas rodas em formato de disco, cada uma com massa m , estão ligadas por uma barra leve, porém rígida de comrpimento l . O conjunto é arremessado de uma superfície horizontal, com velocidade v conform
Determine a força horizontal máxima P que pode ser aplicada ao carrinho de massa M para que a roda não deslize quando começar a rolar sobre o carrinho. A roda tem massa m , raio r e raio de giração k
O cilindro hidráulico B C do caminhão basculante está quebrado e desconectado. O motorista (que fez curso de dinâmica) decide calcular a aceleração mínima a do caminhão necessária para inclinar o depó
Uma bola de boliche de 6,4k g com uma circunferência de 690m m tem um raio de giração de 83m m . Se a bola é lançada com uma velocidade de 6m / s , mas sem velocidade angular quando toca o chão da pis
A porta de garagem suspensa é um painel retangular homogêneo de massa m e é guiada por seus roletes nas extremidades, que correm nos trilhos mostrados (tracejados). Se a porta é liberada a partir do r