Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 103
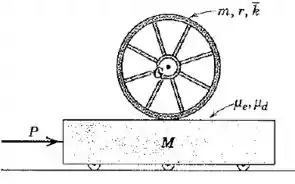
Determine a força horizontal máxima que pode ser aplicada ao carrinho de massa para que a roda não deslize quando começar a rolar sobre o carrinho. A roda tem massa , raio e raio de giração . Os coeficientes de atrito estático e dinâmico entre a roda e o carrinho são e , respectivamente.
Passo 1
Vamos chamar de a aceleração do centro de massa do carrinho. Se aplicarmos a segunda lei de Newton sobre o carrinho na direção horizontal, vamos encontrar o seguinte:
Quais são as forças que agem nessa direção? Primeiro temos a força apontando para a direita.
E segundo, no caso em que a roda não desliza, temos a reação à força de atrito estático entre a roda e o carrinho apontando para a esquerda:
E como a superfície do carrinho é horizontal, podemos escrever a força de atrito da seguinte forma:
E então:
Portanto, a força no caso em que a roda não desliza é:
E todas essas variáveis foram dadas no enunciado, com exceção da aceleração do carrinho, e é ela quem precisamos calcular.
Passo 2
Vamos ver o que conseguimos descobrindo analisando as forças que agem sobre a roda:
Vamos aplicar a primeira lei de Newton na direção horizontal:
E no caso em que não ocorre deslizamento, a força é o atrito estático entre a roda e o carrinho:
E vamos considerar também a soma dos momentos em relação ao centro de massa :
E a única força que produz momento nesse caso é , e o momento de inércia pode ser calculado em função do raio de giração:
Passo 3
E como isso tudo pode se relacionar com a aceleração do carrinho que precisamos achar?
Bom, no caso em que não ocorre deslizamento (apenas rolamento) a aceleração do ponto da roda deve ser igual à aceleração do centro de massa do carrinho:
E a acelerção do ponto pode ser escrita em função da aceleração do centro de massa da roda usando a seguinte fórmula:
E nesse caso, a única aceleração do ponto em relação ao centro de massa está associada à aceleração angular de rolamento:
Agora podemos substituir os resultados que encontramos acima:
Agora é só substituir isso na equação que encontramos no primeiro passo:
Resposta
A força máxima é .