Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 44
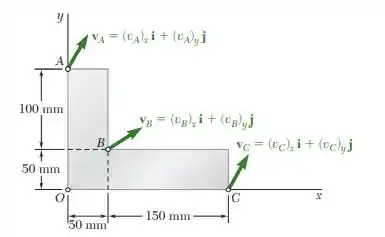
A placa mostrada na figura desloca-se no plano . Sabendo que s, e , determine a velocidade angular da placa, a velocidade do ponto .
Passo 1
Fala aí, galera. Tudo certo? Bora fazer mais questões de Mecânica pra ficar craque. Primeiro, temos que determinar a velocidade angular da placa. Sabemos que o vetor posição é dado por:
E que a velocidade da placa no ponto vai ser dada a partir da seguinte relação:
Substituindo:
Em seguida, podemos agrupar todas as partes da equação que estão relacionadas ao coeficiente . Assim, podemos determinar a velocidade angular da placa, temos:
E então, podemos agrupar também os coeficientes em :
Passo 2
Para determinarmos a velocidade no ponto vamos utilizar as mesmas relações do passo anterior. O vetor posição de vai ser:
E que a velocidade da placa no ponto vai ser dada a partir da seguinte relação:
Substituindo:
Em seguida, podemos agrupar todas as partes da equação que estão relacionadas ao coeficiente . Assim, podemos determinar a velocidade angular da placa, temos:
E então, podemos agrupar também os coeficientes em :
Com isso, temos que a velocidade em vai ser:
Isso é tudo, pessoal. Bora praticar mais!