Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 239

Uma placa plana sela uma abertura triangular na parede vertical de um tanque com líquido de massa específica ρ . A placa bascula em torno da borda superior O do triângulo. Determine a força P necessária para manter a placa em uma posição fechada contra a pressão do líquido.

Passo 1

Aqui devemos calcular o momento resultante devido à pressão da água na placa, e então obter P fazendo o momento em torno do eixo da borda superior que passa por O ser zero. Acharemos o momento causado pela pressão integrando os momentos infinitesimais d M causados por pequenos elementos de altura d y na placa.

Passo 2

O momento causado por um elemento horizontal de distância vertical y até O e altura d y na

Placa é dado por:

d M = y   d F = y ⋅ ρ g h ' d A

A profundidade h ' do elemento será h + y , com y indo de 0 a a . A área d A é dada obtendo o comprimento de cada elemento de coordenada y :

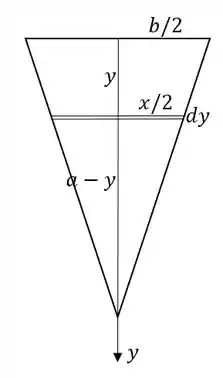
Pela semelhança de triângulos, o comprimento x é dado por:

x / 2 a - y = b / 2 a ⇒ x 2 = b a - y 2 a ⇒ x = b a - y a

x = b - b a y

Então a área infinitesimal d A é

d A = x d y = b - b a y d y

Passo 3

Tendo os valores que precisamos, vamos calcular a integral:

M = ∫ y   d F = ∫ y ⋅ ρ g h ' d A = ∫ 0 a y ⋅ ρ g h + y b - b a y d y

= ρ g ∫ 0 a h b y - h b a y 2 + b y 2 - b a y 3 d y

= ρ g h b 2 y 2 - h b 3 a y 3 + b 3 y 3 - b 4 a y 4 0 a

= ρ g h a 2 b 2 - h a 2 b 3 + a 3 b 3 - a 3 b 4 = ρ g a 2 b h 2 - h 3 + a 3 - a 4

= ρ g a 2 b 3 h 6 - 2 h 6 + 4 a 12 - 3 a 12 = ρ g a 2 b h 6 + a 12 = ρ g a 2 b 2 h + a 12

Passo 4

Então, como o momento em torno de O deve ser zero:

M = P a ⇒ ρ g a 2 b 2 h + a 12 = P a

⇒ P = ρ g a b 2 h + a 12

Resposta

P = ρ g a b 2 h + a 12

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

106- Determine a força e o momento de reação no apoio A para a viga engastada que está submetida a uma carga distribuída senoidal.
113- Uma viga está submetida ao carregamento variável mostrado. Calcule as reações nos apoios A e B.
108- A viga em balanço está submetida a uma carga distribuída parabólica, simétrica em relação ao meio da viga. Determine a força R a e o momento M a atuando na viga em A.
104- A viga está submetida a carga distribuída e ao momento mostrado. Se M for aumentado lentamente a partir de zero, em que valor M 0 o contato em B mudará da superfície inferior para a superior?
109- Determine a força e o momento de reação no apoio A da viga em balanço que está submetida a carga distribuída mostrada.