Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas fundamentais - Ex. 1

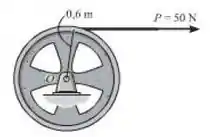
A roda de 80 kg tem um raio de giração em relação a seu centro de massa O, ko = 400 mm. Determine a velocidade angular após haver completado 20 revoluções, partindo do repouso.

Passo 1

Sabendo que a roda parte do repouso (ω1 =0), ou seja, T1 = 0, dado o raio de giração, pode-se determinar o momento de inércia, desse modo:

I o = m × k o

I o = 80 × 0,4

I o = 12,8   k g . m ²

Passo 2

A energia cinética para o estado 2, isto é, alcançado o movimento é dada por:

T 2 = 1 2 I o ω 2

T 2 = 1 2 × 12,8 × ω 2

T 2 = 6,4 × ω 2

Sabendo que a determinação consiste para 20 revoluções, então:

s =   20 × ( ω × r )

s = 20 × 2 π × 0,6

s = 75,398   m

Passo 3

O trabalho será quantificado unicamente devido ao momento aplicado à roda, assim, pelo princípio do trabalho e energia, tem-se que:

T 1 +   ∑ U 1 → 2   =   T 2

0 + M × s = 6,4   × ω 2

50 × 75,398 = 6,4 × ω 2

ω 2 =   50 × 75,398 6,4

ω = 24,3   r a d / s

Resposta

A velocidade angular após completar o total de 20 revoluções será de 24,3 rad/s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda de 50 kg é submetida a uma forca d 50 N. Se a roda parte do repouso e rola sem deslizar, determine sua velocidade angular depois de haver completado 10 revoluções. O raio de giração da roda em
A barra fina uniforme de 25 kg é submetida a um momento de binário M = 150 N.m. Se a barra está em repouso quando θ = 0 ° , determine a velocidade angular quando θ = 90 ° .
A barra fina uniforme de 50 kg está em repouso na posição mostrada, quando P= 600N é aplicada. Determine a velocidade angular da barra quando ela atinge a posição vertical.
A roda de 20 kg tem um rio de giração em relação a se centro O, ko = 300 mm. Quando é submetida a um momento de binário M=50 N.m, ela rola sem deslizar. Determine a velocidade angular da roda após seu
Se a barra fina uniforme de 30 kg parte do repouso na posição mostrada, determine a velocidade angular após haver completado quatro revoluções. As forças permanecem perpendiculares à barra.