Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 126

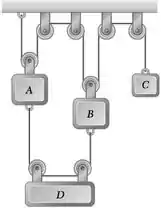
Os blocos A e B têm massa de 20 kg cada, o bloco C de 14 kg e o bloco D de 16 kg. Sabendo a força para baixo de intensidade de 10 g é aplicado no bloco B, e que sistema inicia em repouso, determine em t = 3 s a velocidade (a) de D em relação a A, (b) de C em relação a D. Desprezar o peso das polias e o efeito do atrito.

Passo 1

E a galera tudo certinho? O enunciado pede que a gente determine a velocidade (a) de D em relação a A, (b) de C em relação a D. Desprezar o peso das polias e o efeito do atrito então vem comigo :D

Notem, o sistema está em equilíbrio, vejam as designações das cordas para os cálculos :D

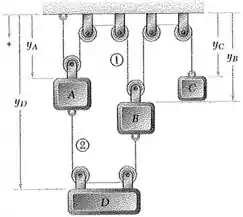
Passo 2

Do diagrama:

Cordão 1:

2 y A + 2 y B + y C = constante

Então

2 v A + 2 v B + v C = 0

2 a A + 2 a B + a C = 0

Cordão 2:

y D = y A + y D = y B = constante

2 v D - v A - v B = 0

2 a D - a A - a B = 0

Passo 3

Determinamos as acelerações dos blocos A, C e D, usando o bloco como corpos livres.

A:

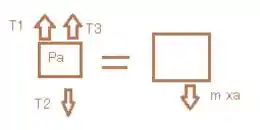
Fazendo o somatório de forças em Y temos :

+ ↓ Σ F y = m A a A :         W A - 2 T 1 + T 2 = W A g a A

20 - 2 T 1 + T 2 = 20 g a A

Passo 4

Em B temos:

+ ↓ Σ F y = m B a B :         W B - 2 T 1 + T 2 + ( F B ) ext = W B g a B

20 - 2 T 1 + T 2 + 10 = 20 g a B

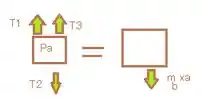
Formando:

3 - 4 ⇒ - 10 = 20 g a A - a B

a B = a A + 1 2 g

Então

Eq.  1 :     2 a A + 2 a A + 1 2 g + a C = 0

E q .   2 :         2 a D - a A - a A + 1 2 g = 0

Passo 5

Em C temos:

a D = a A + 1 4 g

+ ↓ Σ F y = m C a C :         W C - T 1 = W C g a C

T 1 = 14 1 - a C g = 14 1 - 1 g - 4 a A - g = 28 1 + 2 a A g

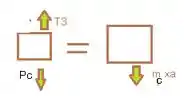
Passo 6

Em D temos:

+ ↓ Σ F y = m D a D :         W D - 2 T 2 = W D g a D

T 2 = 1 2 × 16 1 - a D g = 8 1 - 1 g a A + 1 4 g = 8 3 4 - a A g

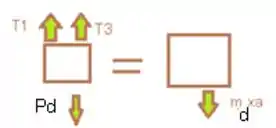
Passo 7

Substituindo T1 [Eq. (5)] e T2 [Eq. (6)] na Eq. (3)

20 - 2 28 1 + 2 a A g + 8 3 4 - a A g = 20 g a A

a A = - 3 14 g = - 3 14 32.2   ft/ s 2 = - 6.90   m / s 2

a C = - 4 - 6.90   m / s 2 - 32.2   m/ s 2 = - 4.60   m/ s 2

a D = - 6.90   m / s 2 + 1 4 - 32.2   m/ s 2 = 1.15   m/ s 2

Nota: Temos movimento uniformemente acelerado, de modo que

v = 0 + a t

Passo 8

  1. Nós temos

v D / A = v D = v A

v D / A = a D t - a A t = 1.15 - - 6.900  m/ s 2   × 3  s

v D / A = 24.2   m/s ↓

Passo 9

v C / D = v C = v D

v c / D = a C t - a D t = - 4.60 - 1.15  m/ s 2   × 3  s

v C / D = 17.25   m/s ↑

Resposta

a)  v D / A = 24.2   m/s ↓

b)  v C / D = 17.25   m/s ↑

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A extremidade A da barra uniforme AB de 8 kg é ligada ao colar que pode deslizar sem atrito na barra vertical. A extremidade B da barra é ligada ao cabo vertical BC. Se a barra é liberada do repouso n
A barra uniforme BD de 300 mm e massa de 4 kg é ligada como mostra a figura à manivela AB e ao colar D de massa desprezível, que pode deslizar livremente ao longo de uma barra horizontal. Sabendo que
Resolva o Problema 16.127 quando θ = 90°.PROBLEMA 16.127 A barra uniforme BD de 300 mm e massa de 4 kg é ligada como mostra a figura à manivela AB e ao colar D de massa desprezível, que pode deslizar
A barra uniforme BD de 3 kg é ligada à manivela BD e ao colar de peso desprezível, que pode deslizar livremente ao longo de uma barra EF. Sabendo que, na posição mostrada na figura, a manivela BD gira
No Problema 16.129, determine a reação em A, sabendo que na posição mostrada na figura a manivela BD gira com uma velocidade angular de 15 rad/s e uma aceleração angular de 60 rad/s2, no sentido anti-