Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 27
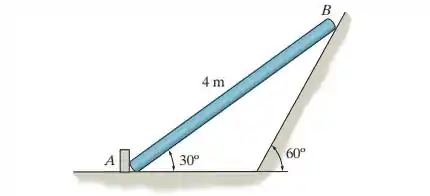
Determine as reações que atuam sobre o elemento uniforme liso, que tem massa de 20 kg.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
A questão pediu para determinarmos as reações das paredes que atuam sobre a barra. Como a superfície de contato é lisa, temos apenas ações de forças normais em relação a cada superfície.
Mas, muito cuidado nessa hora! Percebam que no ponto temos contato com uma superfície vertical e uma superfície horizontal! Portanto, no ponto , temos duas forças normais!
Então, para melhor visualizarmos as forças, suas direções e efeitos, vamos fazer o diagrama de forças. Portanto,
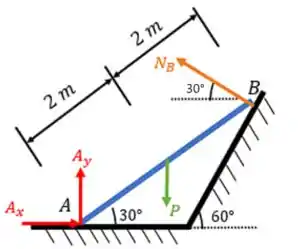
Agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Vamos começar determinando a reação normal no ponto . Para isto, ter que realizar o equilíbrio dos momentos em relação aos pontos .
Sendo assim, temos:
E assim determinarmos a nossa primeira reação!
Passo 3
Agora vamos determinar as reações nos apoios em . Para isto, vamos ter que realizar o equilíbrio de forças nas direções e .
Sendo assim, temos:
Resolvendo o sistema acima, obtemos e .
E assim finalizamos a questão!