Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 33
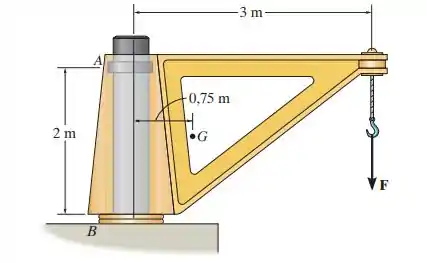
As dimensões de um guindaste, que é fabricado pela Basick Co., são dadas na figura. Se o guindaste tem massa de 800 kg e centro de massa em , e a força máxima prevista para sua extremidade é , determine as reações em seus mancais. O mancal em é radial e apoia somente uma força horizontal, enquanto o mancal em é axial, apoiando componentes horizontal e vertical.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar as reações nos apoios e . Para isto, é fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!!
Sempre que tiverem dúvida, voltem na Tabela 5.1 do livro! Lá são identificados os tipos de apoios com as suas reações!
Então, o nosso diagrama de forças será:
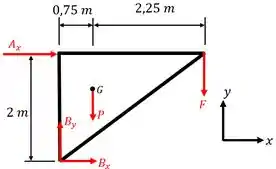
Agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Nosso trabalho agora é aplicar as relações de equilíbrio. Vamos começar trabalhando com o somatório de momentos! Fazendo o somatório em torno do ponto , temos:
E assim descobrimos a reação do mancal !
Passo 3
Agora vamos trabalhar com o somatório de forças! Portanto, realizando o somatório de forças na direção e na direção , obtemos:
Resolvendo o sistema acima, obtemos e .
E assim finalizamos a nossa questão!