Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 119
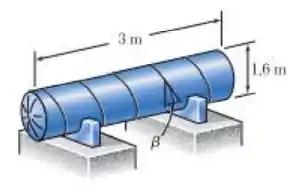
Para o problema , determine o intervalo de valores de que podem ser utilizados considerando que a tensão de cisalhamento paralela à solda não deve ultrapassar 1350 psi quando a pressão manométrica for de .
O tanque de pressão mostrado na figura tem uma parede com espessura de e possui emendas de solda de topo formando um ângulo com um plano transversal. Para uma pressão manométrica de , determine a tensão normal perpendicular à solda e a tensão de cisalhamento paralela à solda.
Passo 1
Fala aí, galera. Beleza? Bora pra mais um exercício.
Primeiramente, sabemos que a tensão normal para tubos de paredes finas sujeitos à pressão, é dada por:
Onde é a pressão interna, é o raio interno e é a espessura da parede. Além disso, a primeira pressão é a pressão na direção radial e a segunda é a pressão na direção axial.
Logo, sabemos que o raio interno é dado por:
Onde . Logo
Onde é a espessura de parede. Portanto, a tensão radial vai ser:
Como a tensão na direção axial é metade dessa, teremos
Agora, basta determinarmos os parâmetros para o círculo de mohr. Temos que a tensão média vai ser dada por:
Este vai ser o centro do círculo e, então, o raio do círculo de mohr vai ser:
Passo 2
E entaão, vamos utilizar a relação para a tensão de cisalhamento paralela à solda, temos:
Onde . Logo, substituindo:
Através do círculo de mohr, teremos dois intervalos possíveis para , São eles:
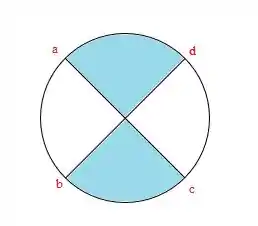
E então, podemos encontrar os valroes de através do arcoseno e, assim, escrever esses intervalos. Fica assim:
Repetindo o processo para os demais pontos do intervalo, temos:
E também:
Assim, o intervalo vai ser:
É isso, galera. Bora fazer mais questões.