Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 102
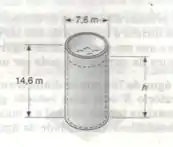
O tanque cilíndrico de armazenamento despressurizado tem uma espessura de parede de e é feito de um aço com de tensão ultima a tração. Determine a máxima altura de água, que pode ser suportada pelo tanque, se um coeficiente de segurança de é desejado. [Peso específico de água = .]
Passo 1
Agora precisamos ficar atentos em, precisamos determinar a máxima altura que podemos aplicar na nossa estrutura, respeitando um coeficiente de segurança de 4,5, para isso sabemos que o nosso fator de segurança é definido como:
Sabemos pelo enunciado que:
Agora precisamos determinar as tensões aplicadas máximas.
- Sabemos que a nossa tubulação é cilíndrica e não esférica, nesse caso, usaríamos as seguintes equações:
- Sabemos que o nosso diâmetro dado, é o diâmetro externo, ou seja, precisamos descontar a espessura, sendo assim temos que:
- E sabemos que é a espessura
- é a pressão que age na no ponto mais baixo da nossa tubulação, e sabemos que para calcular isso, precisamos usar a seguinte equação:
Com isso podemos fazer as nossas contas. Vamos lá?
Passo 2
Sabemos pelo enunciado que:
Calculando o raio, temos que:
Calculando a tensão, teremos que:
Usando o maior valor calculado como tensão aplicada, podemos relacionar isso com o nosso fator de segurança.