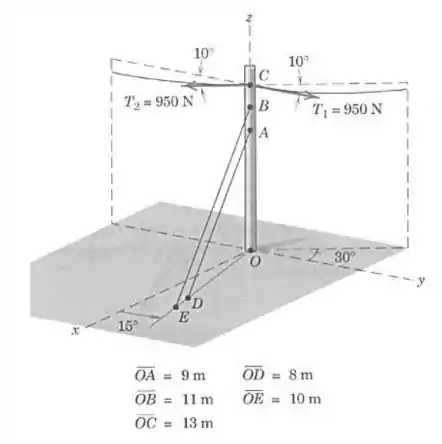
O plano vertical pelo qual passa o cabo de eletricidade gira de no poste vertical . As forças trativas e valem ambas . Para prevenir inclinação do poste com o passar do tempo, os cabos de amarração e são usados. Se os dois cabos são ajustados para suportar forças trativas iguais , as quais, em conjunto, reduzem a zero o momento em , determine a força de reação horizontal resultante em . Determine o valor necessário de . Despreze o peso do poste.

Queremos usar a condição de equilíbrio dos momentos em relação à origem. Mas para isso vamos precisar escrever também os vetores-posição dos pontos de aplicação de cada uma das forças.

Para as duas trações e temos um mesmo vetor  :

E agora para as outras duas (é mais fácil tomar os pontos de aplicação como estando sobre o mastro, mas qualquer ponto na linha de ação da força vai servir):

Agora sim, podemos aplicar a condição de equilíbrio dos momentos:

E a grande vantagem de usar a origem é que possíveis momentos agindo em não aparecem na equação.

Agora vamos calcular cada um desses produtos vetoriais:

E basta considerar uma única componente para encontrar o valor de . Vamos usar a componente , por exemplo:

Agora falta encontrar a força de reação horizontal em . Uma vez que já conhecemos todas as trações isso fica bem mais fácil.

Vamos considerar o equilíbrio das forças no eixo . As expressões vetoriais que nós escremos nos passos anteriores podem ser bem úteis para isso:

E fazendo a mesma coisa para o eixo :

E agora podemos calcular o módulo da força: