Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 75
O centro de massa da porta de está no centro do painel. Se o peso da porta é sustentado inteiramente pela dobradiça inferior , calcule o módulo da força total suportada pela dobradiça em .
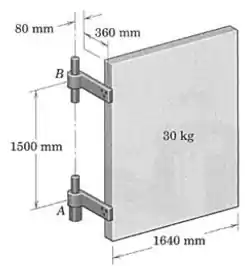
Passo 1
Primeiro vamos definir alguns eixos (não é um sistema de coordenadas comum, são apenas eixos de referência que vamos usar para calcular os momentos):
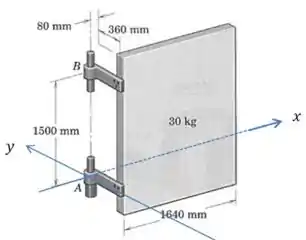
E quais são as forças envolvidas nesse sistema? Não sabemos ao certo a direção das forças nas dobradiças, então vamos dizer que em cada uma existem componentes em todas as direções: em , por exemplo, temos as forças , e .
Só uma observação: como todo o peso da porta é suportado pela dobradiça inferior, não temos uma componente na dobradiça de cima!
Além dessas forças , , , e , temos o peso atuando no centro de massa da placa.
Passo 2
Vamos escolher uma equação de equilíbrio que facilite nosso cálculo (ou seja, que contenha poucas variáveis desconhecidas).
Por exemplo, o momento em relação ao eixo :
Já que as forças , e têm linhas de ação que cruzam o eixo, e é paralela ao eixo.
Passo 3
Agora vamos usar o momento em relação ao eixo . Dessa vez as únicas forças que não terão momento nulo serão e o peso .
Isso acontece porque , e têm linhas de ação que cruzam o eixo e é paralelo ao eixo:
E agora podemos calcular o módulo da força :
Resposta
O módulo da força é .