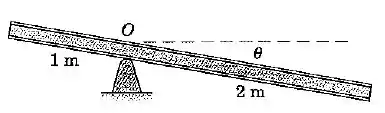
A viga esbelta de possui uma massa de e é liberada a partir do repouso na posição horizontal em . Se o coeficiente de atrito estático entre o suporte fixo junto a e a viga é de , determine o ângulo no qual o deslizamento ocorre pela primeira vez em . O resultado depende da massa da viga.

Agora vamos usar a segunda lei de Newton para determinar o que acontece quando barra está prestes a deslizar.

Na direção tangencial (que é perpendicular à barra), temos a seguinte expressão:

E aceleração tangencial do centro de massa é:

E as forças que agem nessa direção são a normal no ponto e uma componente da força peso:

Na direção normal, que é paralela à barra, temos o seguinte:

E as forças que agem nessa direção são a força de atrito e a outra componente do peso:

E quando a barra está prestes a deslizar, a força de atrito está no seu valor máximo, e portanto:

Substituindo isso na equação que encontramos, ficamos com o seguinte sistema de duas equações:

Dividindo as duas equações:

Então precisamos encontrar para poder resolver o problema.

Queremos encontrar para um certo valor de , sabendo que e . Sabemos também a aceleração angular em função de .

Então vamos nos lembrar da seguinte relação:

E então:

Agora vamos integrar nos dois lados, e substituir a nossa função :

E então vamos substiuir isso na última expressão que encontramos: