Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 81
A ponte consiste de três segmentos que podem ser considerados como pinados em A, D e E, sustentados por apoios oscilantes em C e F e sustentados por rolete em B. Determine as componentes horizontal e vertical da reação em todos esses apoios devido ao peso mostrado.
Passo 1
Começamos desenhando o diagrama do corpo livre dos trecho de interesse:
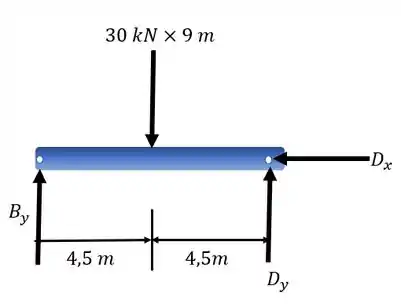
Passo 2
Podemos começar aplicando as equações do equilíbrio em relação ao momento no ponto D para o segmento BD:
Passo 3
Para o mesmo segmento, aplicamos as equações do equilíbrio de forças nos eixos x e y:
Passo 4
Do Diagrama do corpo livre para o trecho da esquerda:
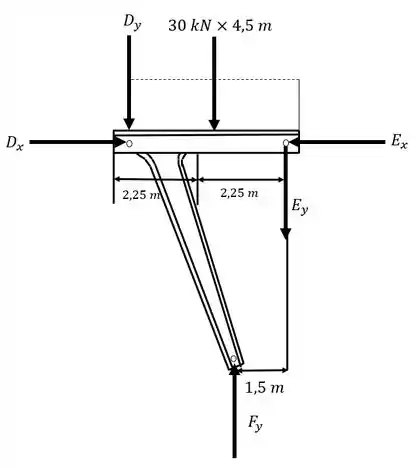
Podemos aplicar a equação do equilíbrio em relação ao momento em relação ao ponto A, com o resultado de :
Passo 5
Aplicando a equação do equilíbrio para as forças no eixo x e y:
Passo 6
Do diagrama do corpo livre do elemento da direita:
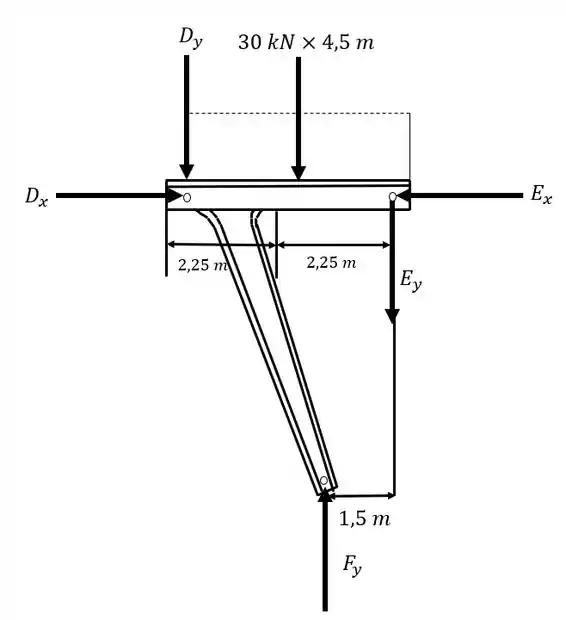
Desse diagrama do corpo livre, podem-se aplicar os resultados obtidos de e obterá:
Passo 7
Podem-se aplicar as equações do equilíbrio de forças nos eixos x e y: