Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 81
81. A porta circular tem peso de e centro de gravidade em . Determine as componentes da reação na dobradiça em e a força que age ao longo da estrutura necessária para manter a porta em equilíbrio. Considere .
Passo 1
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso é uma dobradiça, segundo a tabela do capítulo , seção , esse tipo de conexão por dobradiça exerce força nas três direções dos eixos coordenados e momento em dois eixos.
Abaixo temos um diagrama de corpo livre que vai nos ajudar a ver o que está acontecendo.
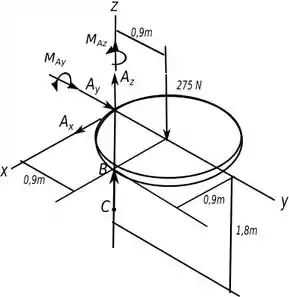
Agora só temos que aplicar as equações de equilíbrio para achar as forças que queremos.
O macete é sempre começar com as equações que te oferecem menos incógnitas.
Para determinar a força ao longo de nessa situação, será melhor expressá-la na forma vetorial, nessa forma teremos as componentes da força do membro, podendo assim usar as equações de equilíbrio para cada direção com a componente adequada da força.
Para expressar essa força, precisamos achar o vetor unitário que tem mesma direção que a força.
Esse vetor pode ser encontrado da seguinte maneira:
Assim no nosso caso temos que o vetor unitário de é:
Agora que temos o vetor unitário, vamos expressar a tração da corda :
Passo 2
Para encontrarmos o valor de , vamos analisar a equação de equilíbrio referente ao momento em relação a
Passo 3
Agora vamos achar as forças que a dobradiça exerce a parti da equação equilíbrio referente a força em relação aos eixos.
Passo 4
Agora vamos descobrir os momentos exercidos pela dobradiça a parti das equações de equilíbrio referentes ao momento em relação aos eixos e .