Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 48
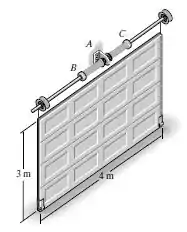
A porta de garagem uniforme tem massa de e é guiada ao longo de trilhos lisos em suas extremidades. A elevação é feita usando-se as duas molas, cada uma das quais fixada ao apoio de ancoragem e ao eixo do contrapeso em e . Quando a porta é elevada, as molas começam a desenrolar do eixo, auxiliando, desta forma, a elevação. Se cada mola fornece um momento torsional , onde está em radianos, deteremine o ângulo no qual ambas as molas, a que desenrola para a esquerda e a que desenrola para a direita, devem ser fixadas, de modo que a porta esteja completamente equilibrada pelas molas, ou seja, quando a porta estiver em posição vertical, e se der a ela um ligeiro impulso para cima, as molas elevarão a porta ao longo dos trilhos laterais até o plano horizontal, sem velocidade angular final. Nota: a energia potencial elástica de uma mola torcional é , onde , e neste caso, .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Podemos aplicar o princípio da conservação de energia analisando o momento incial e final do sistema.
A conservação de energia é dada por:
Vamos analisar cada componente:
Temos também que:
Como o sistema está em repouso no momento inicial, temos que:
Passo 2
Para o momento final, temos:
Temos que . Portanto:
Passo 3
A parcela cinética final também é nula pois nos é dito que , portanto, aplicando conservação de energia, temos: