Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 59
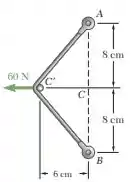
Uma corda elástica é esticada entre dois pontos e , separados de 16 cm no mesmo plano horizontal. Quando esticada diretamente entre e , a tração na corda é de 10 N. A corda é, então, esticada como mostra a figura até o seu ponto médio ser movido de 6 cm para ; uma força de 60 N é necessária para manter a corda em . Uma bolinha de 100 g é colocada em e a corda é liberada. Determine a velocidade que a bolinha passa por .
Passo 1
Vamos lá! Nesta questão precisamos determinar a velocidade que uma bolinha passa por Para isto, iremos utilizar o princípio de conservação de energia, que nos diz que:
De início sabemos que o bloco partirá do repouso. Portanto, . Em relação as energias potenciais, sabemos que temos apenas a contribuição da energia elástica, visto que não há variação na cota da esfera.
Desta forma, substituindo as relações de cada energia, temos:
E agora temos um problemão! Quem é a constante elástica ? E as deformações (relacionada ao comprimento ) e (relacionada ao comprimento )da mola? Este último não podemos calcular pois não sabemos o comprimento sem deformação da mola!
Bom, vamos tratar cada um desses problemas devagar.
Passo 2
Começaremos escrevendo a deformação e a equação da força relativa a cada um dos estados da nossa corda.
Vamos começar pelo estado 2, em que ela está esticada entre os pontos e , mas passando por . Aqui, a deformação é:
E a força, que foi dada na questão, pode ser calculada através da seguinte relação:
E assim chegamos a nossa primeira equação, que correlaciona e o comprimento inicial (e automaticamente né!).
Uma equação, duas incógnitas. Para resolvermos ela, vamos precisar montar um sistema com outra equação. E como faremos isto? Bom, vamos analisar o outro estado da nossa corda!
Passo 3
Agora vamos basicamente repetir o Passo 2, só que para a corda passando pelo ponto . Para auxiliar na visualização da geometria, vejamos um esboço abaixo:
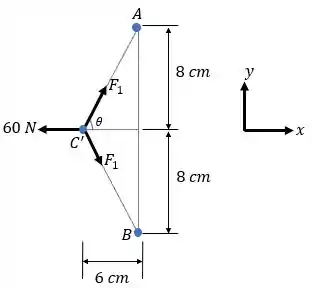
A força que traciona a corda é . Como ela está em equilíbrio, o somatório de forças no ponto é igual a zero. Portanto,
OBS: Calculamos o ângulo através da geometria do problema fazendo .
E assim como fizemos no Passo 2,
E assim chegamos a nossa segunda equação com duas incógnitas!
OBS: O comprimento de 20 cm também foi obtido da geometria do problema (Pitágoras)!
Passo 4
Agora que temos duas equações com duas incógnitas, vamos resolver o nosso sistema para descobrir este comprimento inicial e a constante elástica. Portanto,
Como a corda tem comprimento inicial, sem deformação, de , as deformações e a constante elástica são:
Passo 5
E assim chegamos aos momentos finais da nossa questão. Agora, basta substituirmos os valores obtidos no Passo 4 lá na relação da velocidade que desenvolvemos no Passo 1.
Desta forma,
E assim finalizamos a nossa questão!