Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 62
Um colar de 3 kg pode deslizar sem atrito sobre uma barra vertical e ficar em repouso equilibrando-se sobre uma mola. Ele é empurrado para baixo, comprimindo a mola 150 mm e é liberado. Sabendo que a constante da mola é k = 2,6 kN/m, determine (a) a altura máxima alcançada pelo colar acima de sua posição de equilíbrio, (b) a velocidade máxima do colar.
Fonte: Beer – Dinâmica – 9ª ed
Passo 1
Olá pessoal, tudo bem?
Espero que sim! Bora falar de energia!!
Bem, vamos analisar o problema por conservação de energia.
Temos dois momentos para analisar:
- Quando o colar é empurrado pra baixo e a mola é comprimida em 150 mm e continua em repouso ();
- No instante em que o colar atinge a altura máxima ().
Além de um instante 3, que é o equilíbrio do colar, onde a força da mola e o peso do colar possuem valores iguais.
Podemos analisar através de um pequeno esboço:
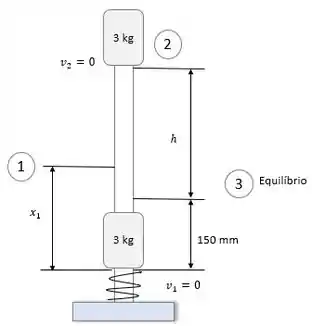
Podemos dizer também que é a deflexão que inclui o comprimento natural da mola e a distância de 150 mm que foi causada pela força inicial para baixo.
Assim, como no problema anterior, podemos assumir, pelo método de conservação de energia:
Passo 2
Letra a) Pronto, já temos nossa expressão principal. Agora vamos reescrevê-la de forma mais esmiuçada, sabendo já que as energias cinéticas nos pontos 1 e 2 são nulas:
Calma, vamos explicar o que foi feito!
Primeiro, vamos descobrir quem é :
Lembra que comentamos que no equilíbrio a força peso do colar se iguala à força elástica da mola? Pois é, podemos encontrar simplesmente por essa igualdade:
Pronto, agora vamos entender o segundo termo da equação 2:
No instante 2, temos equilíbrio, certo??
Sim, temos. Ou seja, A força elástica atuante nesse instante se iguala à alguma “coisa”, e essa “coisa” é o peso do colar. Então podemos muito bem utilizar a energia potencial no momento 2 para analisarmos a conservação da energia.
Então vamos prosseguir, substituindo os valores da equação:
Passo 3
Letra b) Se voltarmos para a figura referente ao problema, podemos imaginar e perceber que a velocidade máxima adquirida pelo colar se dá quando ele passa pelo ponto de equilíbrio (ponto 3 indicado no esboço), e a partir disso, podemos aplicar novamente a conservação da energia. Assim:
Observemos que no instante 3, temos energia potencial elástica e a causada pela força peso. Assim:
Substituindo os valores:
Fazendo o cálculo, encontramos
Resposta
Portanto:
Letra a)
Letra b)