Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 66

Um colar de 1,3 kg pode deslizar ao longo da barra mostrada na figura. Ele está preso a uma corda elástica fixada em F que tem um comprimento indeformado de 0,9 m e uma constante de mola de 60 N/m. Sabendo que o colar é liberado do repouso em A e desprezando o atrito, determine a velocidade do colar (a) em B, (b) em E.

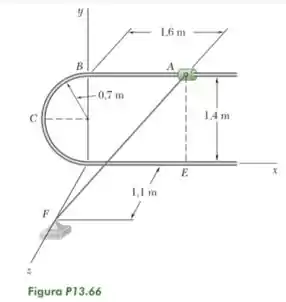
Fonte: Beer – Dinâmica – 9ª ed

Passo 1

Olá pessoal, tudo bem?

Bora lá!!

Bem, vamos analisar o problema de utilizando nossa amiga conservação de energia.

Primeiro, vamos definir o módulo das distâncias de F até A, B e E.

Mas porquê fazer isso??

Porque o problema contempla os 3 eixos de coordenadas!!

É fácil, lembremos que o módulo de um conjunto de vetores é dado pela raiz quadrada da soma dos quadrados, ou seja:

L A F = 1,6 2 + 1,4 2 + 1,1 ²       → L A F = 2,394   m

L B F = 1,4 2 + 1,1 ²       → L B F = 1,78   m

L E F = 1,6 2 + 1,1 ²       → L E F = 1,94   m

Passo 2

Agora vamos as nossas considerações:

  1. Como o problema mesmo disse, v A = 0 .
  2. Podemos comparar o instante em B com o instante em A, que tem energia cinética nula.

Vamos lembrar que a conservação da energia:

E C 1 + E P 1 + E E 1 = E C 2 + E P 2 + E E 2         ( 1 )

Agora é só alegria! A partir dessas análises, vamos para a conservação da energia.

0 + 1 2 k * L A F - 0,9 2 + m g * 1,4 = 1 2 m v B 2 + 1 2 k * L B F - 0,9 2 + m g * 1,4   ( 2 )

Desmembrando a eq. 2, analisando os instantes em A e em B, temos:

0 + 1 2 60 * 2,394 - 0,9 ² + 1 , 3 * 9,81 * 1,4 = 1 2 13 * v B 2 + 1 2 60 * 194 - 0,9 ² + 13 , * 9,81 * 1,4

Substituindo os valores:

1 2 60 * 2,394 - 0,9 2 = 1 2 1 , 3 * v B 2 + 1 2 60 * 1,78 - 0,9 2         →     v B = 8,2   m s

Passo 3

Da mesma forma que encontramos a velocidade em B, podemos encontrar em E através da conservação de energia em comparação ao ponto A.

Agora é só alegria! A partir dessas análises, vamos para a conservação da energia.

0 + 1 2 k * L A F - 0,9 2 + m g * 1,4 = 1 2 m v E 2 + 1 2 k * L E F - 0,9 2                   ( 3 )

Observemos que o ponto E não possui energia potencial gravitacional, uma vez que está no eixo de origem.

Continuando:

Desmembrando a eq. 3, analisando os instantes em A e em E, temos:

1 2 60 * 2,394 - 0,9 ² + 1 , 3 * 9,81 * 1,4 = 1 2 1 , 3 * v E 2 + 1 2 60 * 1 , 94 - 0,9 ²

Assim:

v E = 8,97 m s

Resposta

Portanto:

Letra a) v B = 8,2   m s

Letra b) v E = 8,97 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 18.32 usando a equação de conservação de energia.
No instante mostrado, a barra de 25k g gira no sentido horário a 2r a d / s . A mola fixada em sua extremidade permanece sempre vertical, devido ao rolete guia em C . Se a mola tem um comprimento não
O sistema consiste de dois blocos, A e B , de 30 e 10k g , respectivamente, e das polias de 2,5k g C e D , que podem ser tratadas como dois discos finos. Determine a velocidade do bloco A após o bloco
Uma corrente de massa desprezível está encaixada na engrenagem, que tem massa de 2k g e raio de giração k O = 50m m . Se o bloco de 4k g A é solto do repouso a partir da posição s = 1m , determine a v
O pêndulo consiste de uma barra B A , de 2k g , e um disco de 3k g . A mola está deformada 0,09m quando a barra está na horizontal, como mostrado. Se o pêndulo é solto do repouso e gira em torno do po