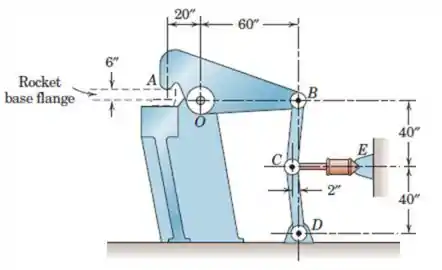
O esboço mostra a configuração aproximada do projeto de um dos quatro conjuntos de retenção de ação alternada que prendem o flange da base de um veículo-foguete ao pedestal de sua plataforma antes do lançamento. Calcule a força de fixação predefinida F em A se o elo CE estiver sob tensão produzida por uma pressão de fluido de 2.000 lb / pol.² agindo no lado esquerdo do pistão no cilindro hidráulico. O pistão tem uma área útil de 16 pol.². O peso do conjunto é considerável, mas é pequeno em comparação com a força de aperto produzida e, portanto, é desprezado aqui.
Passo 1
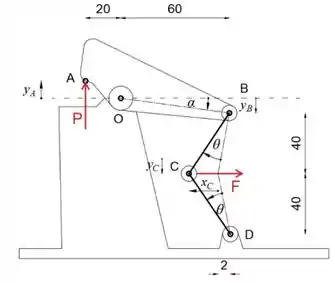
Primeiro, vamos desenhar o diagrama de força ativa
Observe que a magnitude da força F é
Passo 2
Olhando para o esboço, podemos escrever movimentos virtuais dos pontos A, B e C como
Observe que o Movimento Virtual do ponto B na direção y é duas vezes maior que o Movimento Virtual do ponto C na direção y
Substituiremos por e by
Derivaremos ambos lados da equação
Expressaremos delta\alpha como
Passo 3
Trabalho virtual feito pela força F é negativo, pois a direção do movimento é oposta à direção da força
substituiremos por e por
(1)
Trabalho virtual feito por
substituiremos por
Também podemos substituir by
(2)
Passo 4
A seguir, vamos aplicar o Princípio do Trabalho Virtual, que afirma que a soma do trabalho realizado por todas as forças ativas é igual a zero
Substituiremos e pelas expressões (1) e (2) respectivamente
Dividiremos ambos lados da equação por
Podemos expressar P como