A posição de uma partícula é dada por , onde é em metros e é em segundos. Represente graficamente a posição, velocidade e aceleração como funções do tempo para os primeiros segundos de movimento. Determine o instante em que a velocidade é zero.
Passo 1
O enunciado menciona três funções: posição, velocidade e aceleração. Nós podemos obter as duas últimas apenas derivando a primeira!
Para fazer os gráficos, precisamos primeiro achar a função, e depois calcular alguns pontos e traçar a curva.
Passo 2
Começando pela posição, temos:
Uma boa estratégia aqui é calcular apenas nos números pares, o que já é suficiente para traçar um bom esboço.
Posicionando os pontos no plano, o resultado deve ser algo parecido com isso:
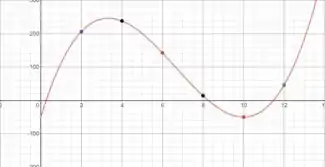
Passo 3
Agora vamos obter a função da velocidade:
E seguindo o mesmo procedimento, o gráfico deve ter essa forma:
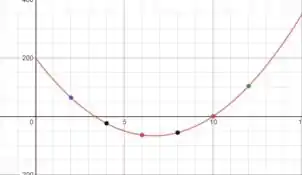
Passo 4
Agora vamos derivar mais uma vez para encontrar a aceleração:
Agora estamos lidando com uma reta, que é bem mais fácil de desenhar: basta ter dois pontos!
O primeiro, e mais fácil, é o ponto onde a reta cruza o eixo , que nesse caso é . E o segundo pode ser qualquer outro. Independente da sua escolha, o resultado deve ser algo assim:
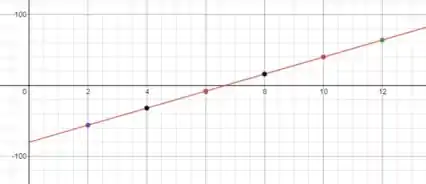
Passo 5
E agora queremos achar o instante em que a velocidade é zero. Nós já achamos esse ponto no passo , mas vamos encontra-lo de outra forma:
Vamos dividir tudo por para facilitar:
E agora podemos procurar as raízes dessa equação quadrática:
E as duas soluções serão:
E nesses dois pontos a velocidade é zero.
Resposta
A velocidade é nula nos instantes e .