O deslocamento de uma partícula que se move ao longo do eixo é dado por , onde é em metros e é em segundos. Represente graficamente o deslocamento, a velocidade e a aceleração contra o tempo para os primeiros segundos de movimento. Determine o instante em que a aceleração é zero.
Passo 1
Vamos começar encontrando as funções da posição, da velocidade e da aceleração. Precisamos lembrar dessa relação:
O enunciado já deu a função . Para encontrar , precisamos derivar:
Aqui precisamos usar a regra do produto para derivar:
Passo 2
E para encontrar precisamos derivar mais uma vez
E precisamos aplicar a regra do produto apenas no segundo termo:
Passo 3
E agora precisamos representar as três funções graficamente nos primeiros segundos:
Esse é um gráfico bem mais difícil de desenhar: é melhor fazer numericamente!
Começando pela , vamos calcular alguns pontos, colocá-los no gráfico e desenhar uma curva de comportamento exponencial:
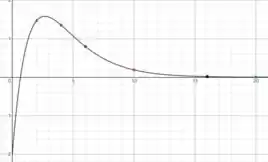
Nesse caso apenas pontos foram suficientes para fazer um bom esboço.
Passo 4
Para fazer os outros dois gráficos você tem duas opções: resolver numericamente também ou traçar a derivada no “olhômetro”.
Vamos traçar o gráfico da velocidade numericamente, não é preciso calcular muitos pontos:
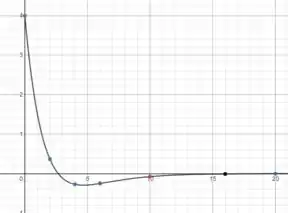
E fazendo a mesma coisa para a aceleração:
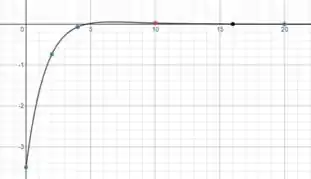
Passo 5
O próximo passo é determinar o instante em que a aceleração é zero. Retomando a nossa função:
E igualando a zero:
A exponencial nunca vai ser igual a zero, então podemos dividir ambos os lados por :
E esse é o instante em que a aceleração é nula.
Resposta
A aceleração é zero no instante .