Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 120
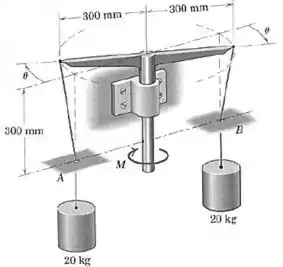
A posição vertical dos dois cilindros de é controlada pelo momento aplicado ao eixo central. Os cabos presos às extremidades dos braços passam por furos lisos em e , situados em uma superfície fixa. Faça um gráfico de como função de desde até . Determine o valor máximo de e o valor correspondente de . Considere em seus cálculos.
Passo 1
Os cabos que passam pelos furos lisos transmitem o peso das massas de para as extremidades dos braços:
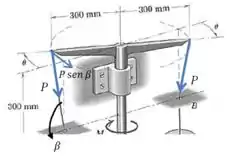
Mas perceba que a componente não é tangente ao círculo! E sabemos que o ângulo que a força forma com a direção tangente é , por isso a componente de que é perpendicular aos braços é:
E então as duas forças formam um binário, separadas por uma distância , então:
Passo 2
Mas queremos o momento apenas em função de , e então precisamos encontrar outra forma de representar .
Olhando para a imagem que desenhamos no passo , vamos primeiro usar o teorema de pitágoras para encontrar o comprimento da hipotenusa que passa por :
E então segue a seguinte fórmula:
Passo 3
Vamos substituir isso na equação para o momento:
Agora perceba que também é igual a , então:
E :
E agora podemos representar isso em um gráfico:
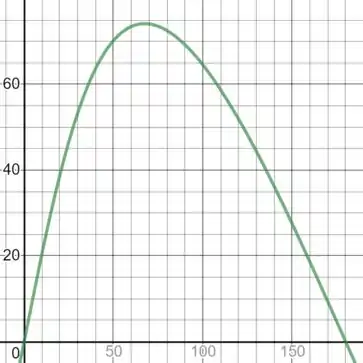
E usando o mesmo gráfico podemos calcular o ponto máximo:
Resposta
O valor máximo de é , que corresponde ao ângulo .