85. A placa circular possui um peso e centro de gravidade em seu centro. Se ela é sustentada por três cordas verticais presas à sua borda, determine a maior distância a partir do centro em que qualquer força vertical pode ser aplicada de modo a não fazer a força em qualquer um dos cabos se tornar zero.
Passo 1
Para resolver esse problema primeiro temos que avaliar o diagrama de forças e ter a seguinte sacada de passar um eixo que passa por e e analisar a equação de equilíbrio referente ao momento em relação a esse eixo , mas esse eixo poderia ser traçado entre qualquer dois pontos desse disco onde tem as cordas.
Com isso para acharmos podemos considerar e achar para que essa situação ocorra, e como foi dito antes, podemos traçar o eixo entre quaisquer dois pontos onde têm cordas. Então se acharmos para essa situação teremos para qualquer outra.
Abaixo temos o diagrama de força para essa situação.
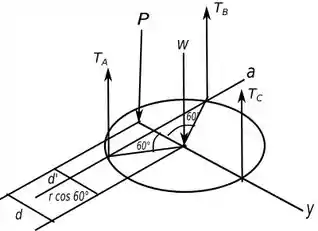
Passo 2
Vamos analisar a equação de equilíbrio referente ao momento em relação ao eixo .
Passo 3
Agora que temos quanto vale temos como achar :