Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 84
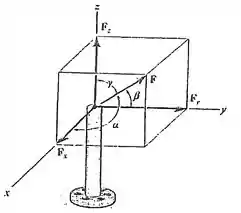
O poste está submetido à força , que tem componentes atuando ao longo dos eixo , , , como mostra a figura. Se a intensidade de é kN, e , determine as intensidades de suas três componentes.
Passo 1
Vamos começar encontrando nosso terceiro ângulo de direção coordenada, como já temos dois, achamos o terceiro pela relação:
Assim:
Passo 2
Como já temos os ângulos e a intensidade, basta apenas encontras as componentes dado:
Então:
Resposta
Exercícios de Livros Relacionados
Expresse F1 e F2 como vetores cartesianos.
Determine a projeção da força F ao longo do poste.
O cabo exerce uma força de 250 N sobre a lança do guindaste, como mostra a figura. Expresse F como um vetor cartesiano.
Determine o ângulo θ entre B A e B C .
Determine a projeção da força F ao longo do poste.