Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 172
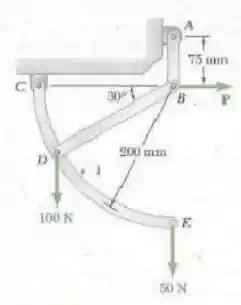
Para o sistema e o carregamento mostrados na figura, determine a força necessária para o equilíbrio, a força correspondente no elemento , a reação correspondente em .
Passo 1
Para respondermos essa questão vamos começar analisando a parte curva da nossa estrutura que engloba os pontos , aplicando as condições de equilíbrio vamos encontrar
Passo 2
Por fim, para o corpo teremos
Resposta
Exercícios de Livros Relacionados
A haste suporta um cilindro com massa de 50k g e tem um pino em sua extremidade A . Se ela estiver sujeita a um momento de binário de 600N ⋅ m , determine o ângulo θ para que haja equilíbrio. A mola t
A viga está sujeita às duas cargas concentradas. Supondo que o alicerce exerça uma distribuição de carga linearmente variável em sua base, determine as intensidades de carga w1 e w2 para que haja equi
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.1. Determine as componentes horizontal e vertical da reação dos apoios. Despreze a espessura da viga.
Determine as reações nos suportes A e B para que a viga fique em equilibrio.
Determine as componentes horizontal e vertical da reação no pino A, e a reação no rolete em B sobre a alavanca.