Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 3
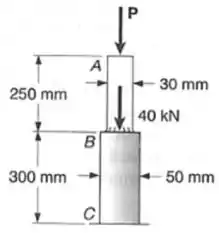
No Prob. 1.2, determine a intensidade da força para que a tensão normal seja a mesma em ambas as barras.
Passo 1
O problema pediu o valo da força para que as tensões normais nas barras AB e BC sejam iguais. A gente sabe que a tensão normal é dada por:
Lembra que esse da fórmula é diferente do do problema. No problema é apenas uma força externa, na fórmula é a força interna que atua na barra (de tração ou compressão). Ambos os “P” podemos ser iguais ou não.
Se a gente quer que as tensões sejam iguais, então vamos ter algo da forma:
Passo 2
Vamos achar as forças internas e , para isso temos de achar a força que atua em e deixa a barra em equilíbrio:
Repare que aqui a força foi colocada de baixo para cima por uma questão de conveniência, porque a gente sabe que para equilibrar a barra a força deve ser apontada para cima. Mas o sentido dessa força não importa, é pura convenção!! Caso o sentido esteja certo acharemos um valor positivo, caso esteja errado acharemos um valor negativo o que significa que o sentido deve ser trocado.
Como só temos forças na vertical vamos ter que o somatório das forças em é igual a zero:
Vamos considerar o sentido positivo para cima, logo teremos:
Passo 3
Vamos fazer o corte na barra AB para achar
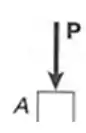
Para permanecer em equilíbrio e achar a nós temos de adicionar a força interna:
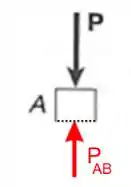
Agora sim! A força que a gente realmente quer é a que atua bem no corte! E não precisa de muito para ver que (em módulo pelo menos né), além disso fica bem nítido que a barra está sob efeito de compressão (olha como e “amassam” a barra).
Daí temos que
Ficou meio esquisito (e óbvio) porque o problema fornece as mesmas letras para a fórmula e a força externa, mas nada demais também.
Passo 4
Agora vamos fazer os mesmos passos para achar a força . Então primeiro vamos achar a força interna que atua na barra BC, para tanto vamos fazer um corte em BC:
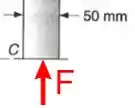
Nós já sabemos que a força , mas pelo desenho percebe-se que ainda falta aquela “forcinha” que atua no interior da barra né? Então vamos desenha-la
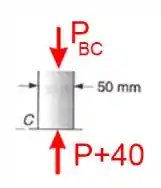
Chamei aqui a força que atua dentro da barra de e é nítido que ela é igual a , porque a barra permanece em equilíbrio:
Passo 5
Agora que temos as forças internas, podemos voltar para a equação da tensão:
Onde:
Assim,
Como e 4 se encontram nas mesmas posições dos dois lados nós podemos cortá-los:
Passo 6
Resolvendo essa equação:
Multiplicando cruzado