Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 118
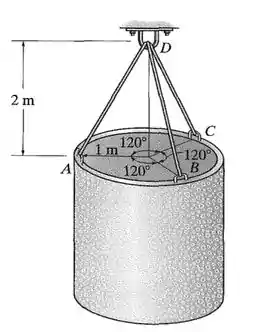
O tubo de concreto de está suspenso por três cabos. Se os diâmetros de forem e tiver diâmetro de , determine a tensão normal média em cada cabo.
Passo 1
Desejamos encontrar o valor da tensão média em cada um dos cabos e para isso devemos levar algumas coisas em consideração. Primeiramente, calculemos o peso desse bloco assim
O ângulo que nos interessa é a metade do ângulo destacado na figura, ou seja, .
Passo 2
Das equações de equilíbrio do nosso corpo vamos ter
Da simetria do problema podemos concluir que . Calculando agora o somatório das forças no eixo vamos obter
Assim, vamos ter, calculando a tensão normal média
Resposta
Exercícios de Livros Relacionados
No Prob. 1.2, determine a intensidade da força P para que a tensão normal seja a mesma em ambas as barras.
Para a estrutura do Prob. 1.6, determine o diâmetro externo d necessário para as arruelas, sabendo-se que a tensão normal axial em cada parafuso é de 20M P a e que a tensão normal de esmagamento média
A haste de ligação AC do problema 1.11 tem uma seção transversal retangular uniforme de 3,2 mm de espessura e 25,4 mm de largura. Determine a tensão normal na porção central da haste, quando α = 9 0 °
Cada uma das quatro hastes verticais, ligadas às duas barras horizontais, tem uma seção transversal uniforme de 10 × 40m m e os pinos tem diâmetro de 14 mm. Determine o máximo valor da tensão normal m
Sabendo-se que a haste de ligação BD tem uma seção transversal uniforme, de área igual a 800m m ² ², determine a intensidade da carga P para que a tensão normal na haste BD seja 50M P a .